Cálculo de la matriz inversa por determinantes

26.   Sea  la  matriz 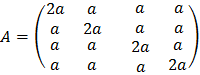  .  Encuentra  su  inversa,  si  existe,  cuando a = 1.

27.   Dada la matriz  .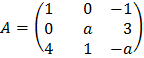

a)   Halla los valores de a para los cuales la matriz A tiene inversa.

b)   Para a = 2, calcula la inversa de A.

28.   Calcula x para que estas matrices tengan inversa. Determina la inversa cuando exista.

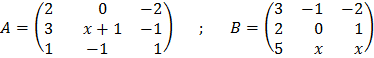
29.   Siendo las matrices    y  .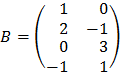

a)   ¿Es cierto que det (AB) = det (BA)?

b)   Calcula, si es posible, la inversa de AB. 

30.  Demuestra que  , siendo: 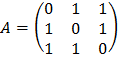 , e I la matriz identidad de orden 3. Calcula    aprovechando la igualdad anterior.

31.   Halla la matriz X² + Y², siendo X e Y las soluciones del siguiente sistema matricial:

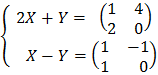
32.   Resuelve las siguientes ecuaciones matriciales siendo A, B y C las siguientes matrices:

a)                                          b)                                                      c)

d)                           e)                                             f)

33.   Dadas las siguientes matrices cuadradas de orden 2:

Calcula:

a)   La matriz inversa de P, es decir,  .

b)   La matriz real cuadrada X de orden 2, tal que  .

c)   La matriz cuadrada  .