Cálculo del rango por determinantes

16.   Calcula, por determinantes, el rango de las siguientes matrices:

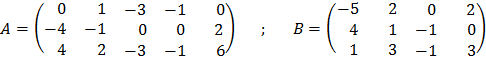
17.   Calcula, por determinantes, el rango de la matriz A según los valores de k:

18.   Calcula x para que el rango de estas matrices sea 3:

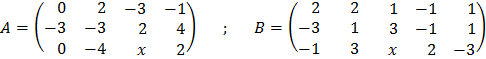
19.   Halla el rango de la siguiente matriz según los valores de :

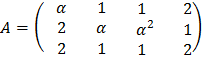
20.   Estudia el rango de las siguientes matrices según los valores del parámetro que contienen:

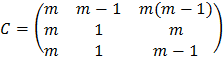
21.   Encuentra los valores de m y n que hacen que estas matrices tengan:

a)   Rango A = 2 y rango B = 3.

b)   Rango A = rango B = 2.

c)   Rango A = rango B = 3.

22.   Estudia el rango de la matriz siguiente:

23.   Dadas        las       matrices              y       ,      ¿es      cierto      que

       rango (AB) = rango (A)·rango (B)? Justifica la respuesta.

24.   Responde razonadamente:

a)   Si una matriz A tiene inversa, ¿cuál es el rango de  ?

b)   ¿Es cierto siempre que  ?

c)   ¿Es     cierto     siempre     que,     si     A    y    B    son    matrices    de    la    misma    dimensión,     ?

d)   ¿Y que  ?

25.   Dadas las matrices    y  . Determina los valores de c tales que la matriz   no tenga rango 2 y di en cada caso cuál es el rango para esos valores de c.