Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2025

PREGUNTA 4. GEOMETRÍA. (2,5 puntos). Responda uno de estos dos apartados: 4.1. o 4.2.

4.1. Determine el valor que debe tomar k para que los planos:

sean paralelos. Calcule también el valor de k que hace que esos mismos planos sean perpendiculares.

4.2. Considérense el punto P(0, 1, 0) y la recta .

4.2.1. Determine la ecuación continua de la recta s que es paralela a r y pasa por el punto P.

4.2.2. Obtenga la ecuación implícita o general del plano  que pasa por P y es perpendicular a r.

 

4.1.  Si los planos son paralelos los vectores normales de los mismos también lo son.

  

 

 

 

 

 

 

 

 

 

 

 

Si los planos son perpendiculares, los vectores normales también lo son:

 

 

 

 

 

 

 

 

 

 

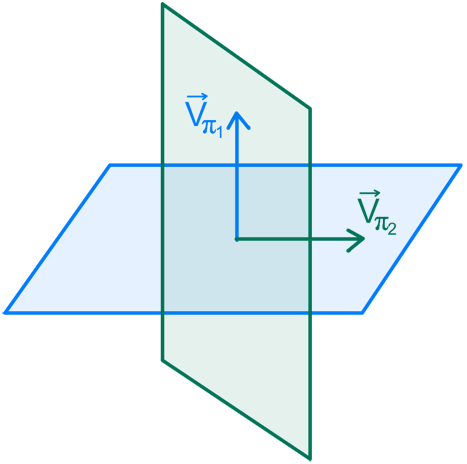
4.2.   

4.2.1. Primero obtenemos un punto y el vector director de la recta r:

 

 

Como la recta s tiene que ser paralela a la r, tiene el mismo vector director y nos dicen que tiene que pasar por el punto P:

 

 

 

 

4.2.2. Para que el plano sea perpendicular a la recta, los vectores normal del plano y director de la recta deben ser paralelos:
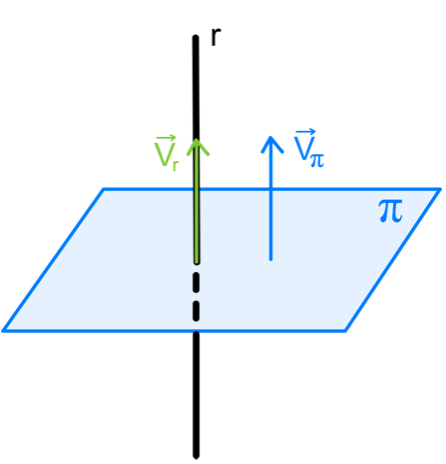