Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2025

PREGUNTA 3. ANÁLISIS. (2,5 puntos). Responda uno de estos dos apartados: 3.1. o 3.2.

3.1. Dada la función , se pide responder a las siguientes cuestiones:

3.1.1. ¿Qué condición deben cumplir k y m para que f sea continua en x = 1?

3.1.2. ¿Para qué valores de k y m es f derivable en x = 1? 

3.2. Dibuje la región encerrada por la gráfica de , el eje X y las rectas x = 0, x = 4. Luego, calcule su área.

 

3.1.   

3.1.1. La función f(x) es continua en  porque las dos partes de esta es una función son polinómicas y, por lo tanto, continuas. Para que la función sea continua, debe serlo también en el punto x = 1:

 

 

 

 

 

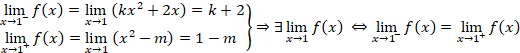
3.1.2. Para  que  una  función  sea  derivable  tiene  que  ser  continua,  por  lo tanto, debe cumplir la ecuación obtenida en el apartado anterior. Estudiemos ahora la derivabilidad. Como la función es continua en ese punto, puede ser derivable. Lo comprobamos:

 

 

 

 

 

 

 

 

Habiendo calculado el valor de uno de los parámetros calculamos el otro en la condición que teníamos para que la función fuera continua:

 

 

La función es continua y derivable si    y  .

 

3.2. Tenemos que representar una función irracional. En estas funciones el dominio es el conjunto de valores que hace que la expresión que tenemos dentro de la raíz cuadrada sea positiva o igual a cero, ya que en caso contrario no podríamos calcular la raíz:

 

 

Así pues, . Calculamos los puntos de corte:

 

Corte eje X:

 

 

Corte eje Y:

 

 

 

Con estes datos podemos hacer la gráfica de la función:

 

 

 

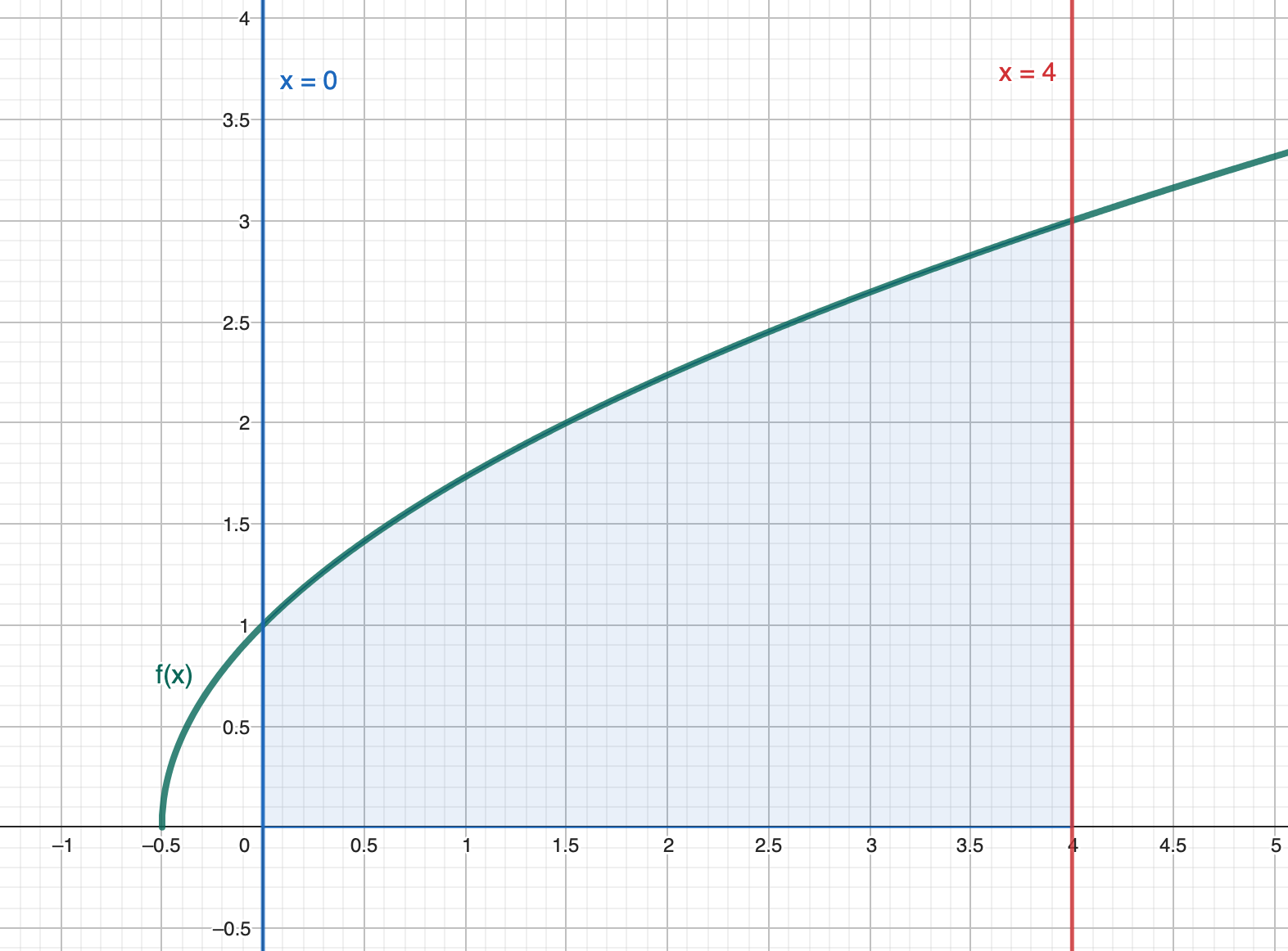
Para calcular el área encerrada por la función, las dos rectas verticales y el eje X (sombreada en azul) planteamos la siguiente integral definida:
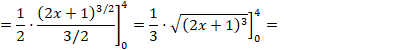