Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2025

PREGUNTA 2. NÚMEROS Y ÁLGEBRA. (2,5 puntos). Responda uno de estos dos apartados: 2.1. o 2.2.

 

2.1. Responda a las dos cuestiones siguientes:

 

2.1.1. Si  ,   halle     tales  que  ,   donde  I  y  0   son   las

 

           matrices identidad y cero, respectivamente.

2.1.2. Calcule la matriz cuadrada X tal que , si  y . ¿Son iguales  y ?

 

2.2. Discuta, según los valores del parámetro m, el sistema:

 

 

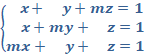
2.1.   

2.1.1. Para calcular los parámetros pedidos, primero calculamos la matriz cuadrada de A:

 

Sustituimos las matrices en la ecuación y operamos:

 

Para que dos matrices sean iguales deben serlo cada uno de sus elementos. Así entonces, igualamos:

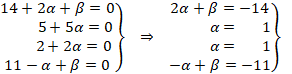
De las ecuaciones del medio obtenemos el mismo valor de alfa y con ese valor, calculamos beta en las otras dos ecuaciones:

Según lo calculado  y  para que se cumpla la ecuación propuesta.

 

2.1.2. Primero despejamos X en la ecuación matricial:

Ahora calculamos la inversa de la matriz A: 

 

Por último, calculamos la matriz X: 

Las matrices X·A y A·X no son iguales ya que el producto de matrices no cumple la propiedad conmutativa. Solo podrían dar lo mismo si una fuera la inversa de la otra, cosa que sabemos que no es así, ya que calculamos la inversa de A. De todas formas, se puede comprobar haciendo las multiplicaciones: 

 

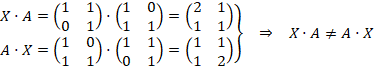
2.2.  Planteamos dos matrices, la de coeficientes (A) y la ampliada con los términos independientes (A^*): 

 

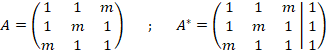
Calculamos el determinante de la matriz A para determinar su rango. I:

 

 

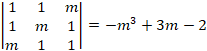
Igualamos a cero el determinante para saber qué valores de m lo anulan:

 

 

 

 

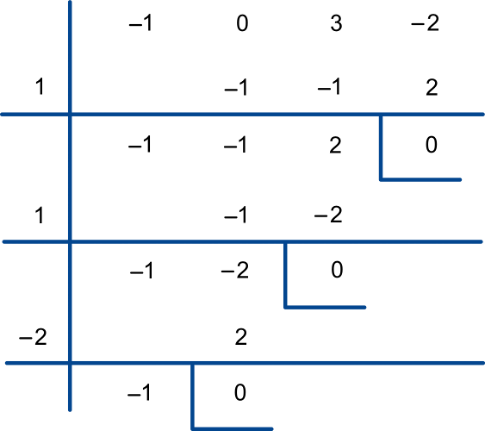
Obtenemos una raíz doble y una simple:

 

 

El rango de la matriz A será:

 

· Si  .

 

· Si  , ya que encontramos algún determinante de este orden distinto de cero:

 

· Si  , ya que todos los determinantes de orden 2 son cero, pero sí tenemos elementos distintos de cero.

 

Los casos que tenemos entonces serían los siguientes:

 

· Si 

 

El rango de la matriz ampliada es 3, porque el determinante de A, que era distinto de cero, también está en la matriz ampliada.

 

· Si 

 

El rango de la matriz ampliada es 3 porque hay algún determinante de este orden distinto de cero:

 

 

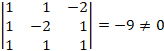
· Si 

 

El rango de la matriz ampliada es 1 porque todos los determinantes de orden 2 y 3 son nulos.