Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Junio 2025

4.2. Una encuesta realizada a 100 individuos de una población revela que 80 de ellos están satisfechos con el servicio de su compañía eléctrica.

4.2.1. Calcule un intervalo con un 95% de confianza para la proporción de individuos satisfechos con el servicio de su compañía eléctrica.

4.2.2. Si se sabe que 8 de cada 10 individuos están satisfechos con el servicio de su compañía eléctrica y se toma una muestra de 100 individuos, ¿cuál es la probabilidad de que la proporción de individuos satisfechos con el servicio de su compañía eléctrica sea superior al 87%?

 

4.2.1. Sea “p = proporción (poblacional) de individuos de una población satisfechos con el servicio de su compañía eléctrica”

 

Tenemos que, siendo    el estadístico proporción de individuos satisfechos con el servicio de su compañía eléctrica (en una muestra aleatoria) sería:

 

 

Vamos a calcular, a partir del nivel de confianza, :

 

 

 

 

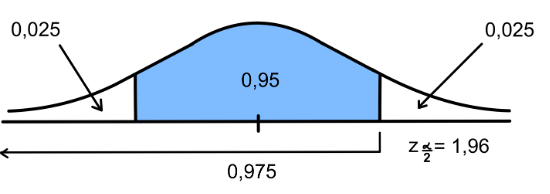
Si vamos a la tabla de la normal, el valor de z que deja detrás de sí una probabilidad de 0,975 es 1,96.

 

A partir de la expresión del nivel de confianza para la proporción, calculamos la proporción de individuos satisfechos con los servicios de su compañía eléctrica con este nivel de confianza:

 

 

 

 

La proporción de individuos de una población satisfechos con su compañía eléctrica se sitúan entre 0,7216 y 0,8784 con un nivel de confianza del 95%.

 

 

4.2.2. Como nos dicen que 8 de cada 10 individuos están satisfechos con los servicios de su compañía eléctrica, conocemos el valor de la proporción poblacional:

 

 

Sea  la proporción de individuos satisfechos con los servicios de su compañía eléctrica, en muestras de 100 individuos. Por lo tanto:

 

 

Ahora, la probabilidad que nos piden será:

 

 

 

 

La probabilidad de que la proporción de personas de una población, de una muestra de 100 individuos, estén satisfechas con los servicios de su compañía eléctrica sea superior al 87% es de 0,0401.