Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Junio 2025

3.2. Dada la función , siendo a, b números reales.

3.2.1. Calcule a y b sabiendo que dicha función pasa por el punto (4, 5) y tiene un mínimo en x = 1.

3.2.2. Para  y , calcule el área limitada por f(x) y la recta .

 

3.2.1. Si la función pasa por el punto (4, 5), se cumple:

 

 

 

Como tiene un mínimo en x = 1, se cumple que la primera derivada se anula en ese valor:

 

 

 

La otra condición, que nos permite calcular otra ecuación, es la de que los máximos (también los mínimos) son puntos donde se anula la primera derivada:

 

 

 

 

3.2.2. Para los valores obtenidos para los parámetros, la función nos queda:

 

 

Primero vamos a calcular los puntos de corte de la función y la recta que nos dan:

 

 

 

Representamos la parábola y la recta e identificamos el área que tenemos que calcular:

 

 

 

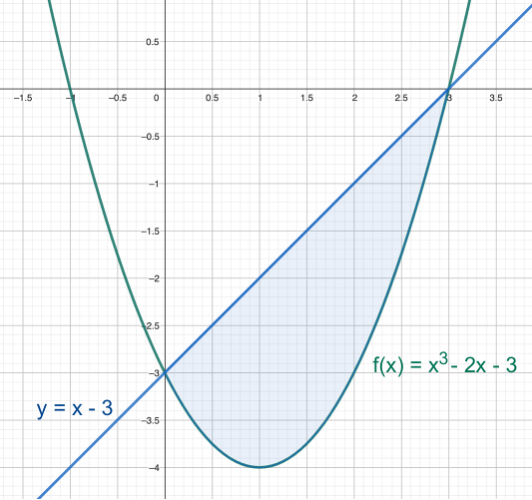
Para calcular el área planteamos la integral de la función que encierra esa área por la parte superior (la recta) menos la que lo hace por la parte inferior (la parábola) entre los puntos de corte calculados anteriormente:

 

 

 

 

El área encerrada por la parábola y la recta es: