Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Junio 2025

EJERCICIO 3. ANÁLISIS. (2,5 puntos)

 

Responda uno de estos dos apartados: 3.1. o 3.2.

 

3.1. Dada la siguiente función:

 

 

3.1.1. Estudie el crecimiento y decrecimiento de la función y sus máximos y mínimos, si existen.

3.1.2. Estudie sus intervalos de concavidad y convexidad y sus puntos de inflexión, si existen.

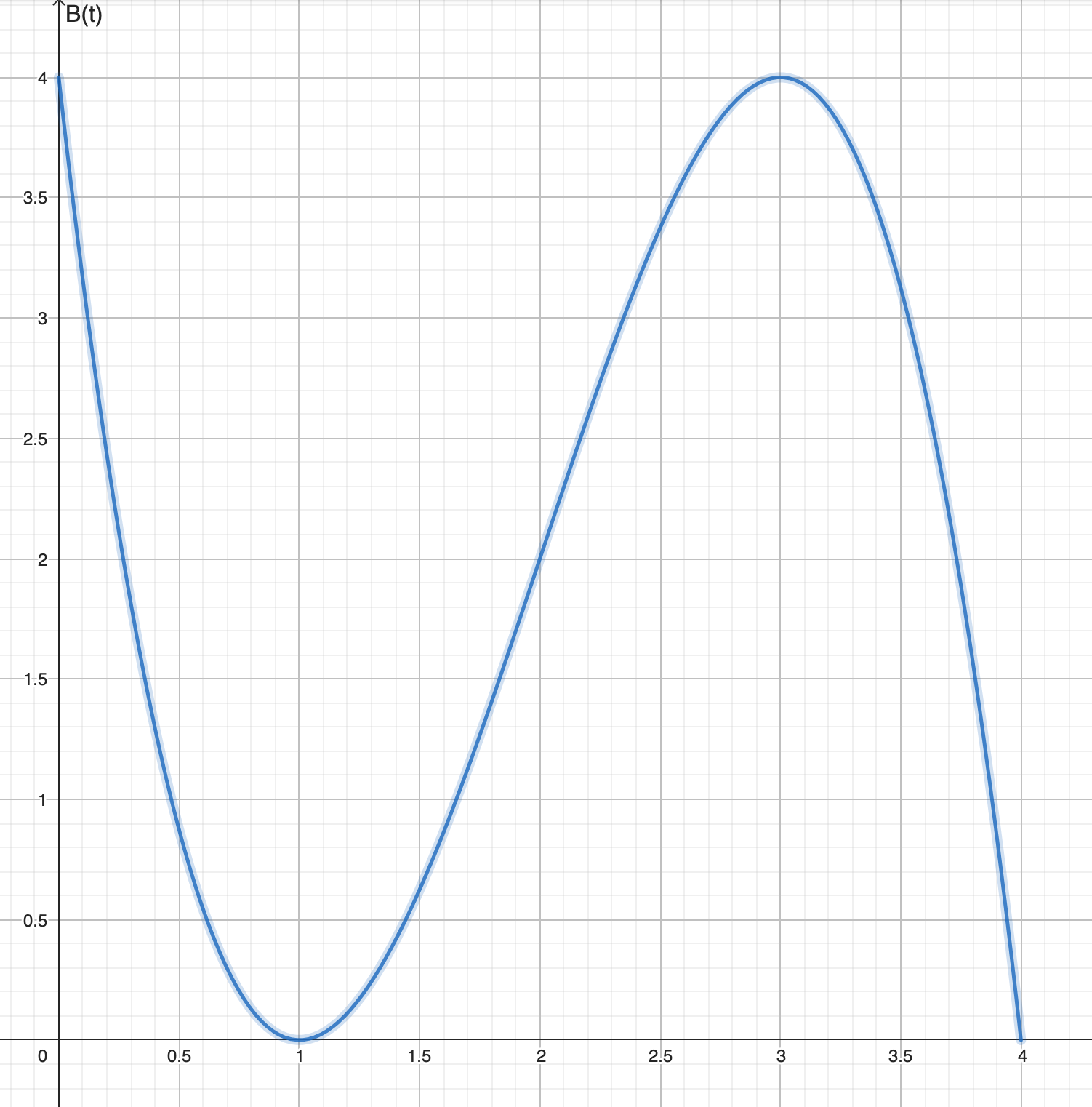
3.1.3. Represente la gráfica de la función B(t).

 

3.1.1. Para estudiar el crecimiento y decrecimiento hacemos la primera derivada de la función e igualamos a cero para obtener los puntos críticos:

 

 

 

 

 

 

Los dos puntos están en el dominio de definición de la función. En los intervalos resultantes miramos el signo de la primera derivada:

 

 

 

 

 

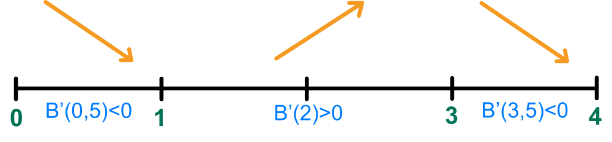
Tanto los extremos del intervalo como los puntos críticos pueden ser máximos o mínimos, para comprobarlo calculamos la imagen de los mismos:

 

 

 

 

 

Como vemos la función presenta dos máximos absolutos en los puntos (0, 4) y (3, 4) y dos mínimos absolutos en los puntos (1, 0) y (4, 0).

 

 

3.1.2. Para calcular los posibles puntos de inflexión hacemos la segunda derivada y la igualamos a cero:

 

 

 

 

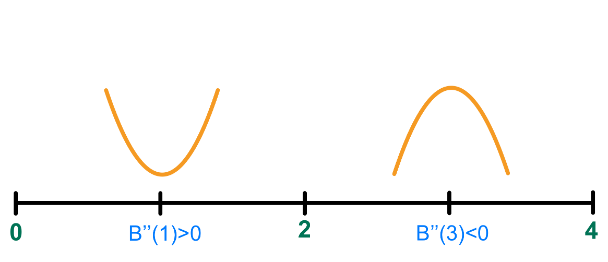
Estudiamos el signo de la segunda derivada teniendo en cuenta el dominio y el posible punto de inflexión:

 

 

 

 

En el punto x = 2 cambia la curvatura, calculamos la imagen de este punto.

 

 

La función tiene un punto de inflexión en el punto (2, 2).

 

 

3.1.3. Con todo lo calculado resulta sencillo dibujar la gráfica de la función: