Galicia. Examen EBAU resuelto de Física. Junio 2025

El examen consta de 4 preguntas de respuesta obligatoria, puntuadas cada una con 2,5 puntos. La primera, más competencial, sin apartados optativos. Las otras tres con un primer apartado de respuesta única y un segundo apartado con dos problemas a elegir uno.

 

PREGUNTA 1. INTERACCIÓN GRAVITATORIA. (2,5 puntos)

 

El satélite SpainSat NG I, de la empresa española Hisdesat, se lanzó con éxito desde Cabo Cañaveral a las 2:34 del 30 de enero de 2025, a bordo del cohete Falcon 9 de la empresa SpaceX. El lanzamiento marca un hito importante en la colaboración espacial europea: mientras Hisdesat ha liderado el desarrollo del satélite, la Agencia Espacial Europea (ESA) ha encabezado la creación de su avanzada carga útil de comunicaciones, que cuenta con una innovadora tecnología de antenas que permite una transmisión de datos más rápida, una mayor seguridad y la capacidad de dirigir con precisión los haces de comunicación allí donde sea necesario.

Con un peso de 6,1 toneladas y una altura de 7,2 metros, el nuevo satélite lleva un equipo especial que lo protege de las interferencias y garantiza que las comunicaciones sigan siendo privadas y seguras. Tras el lanzamiento, el satélite viajará hasta su posición final en órbita geoestacionaria a 35 786 km sobre la Tierra, casi tres veces el diámetro de la Tierra misma. Una vez en su lugar, se someterá a pruebas de aceptación en órbita antes de entrar en funcionamiento.

Usted forma parte del equipo del SpainSat NG I que tiene que hacer los cálculos para controlar el satélite en su órbita por lo que:

 

1.1. Responda estos tres apartados. (1 punto)

1.  Dibuje un esquema de la órbita del satélite, indicando la dirección y el sentido de la fuerza gravitatoria que experimenta el satélite.

 

La fuerza gravitatoria actúa como fuerza centrípeta y haciendo que el satélite gire en una órbita circular:

 

 

 

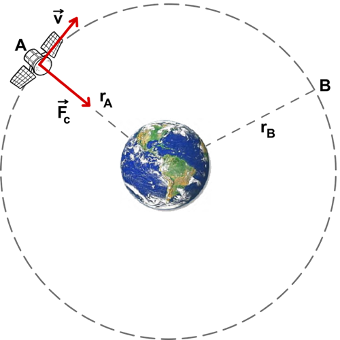
2.  Calcule la aceleración gravitatoria que experimenta el satélite.

 

Calculamos el módulo del campo gravitatorio:

 

 

 

 

3.  Calcule la velocidad del satélite en su órbita.

La expresión que nos permite calcular la velocidad del satélite en la órbita se obtiene justamente de que la fuerza gravitatoria es una fuerza centrípeta:

 

 

 

 

 

1.2. Indique y justifique la respuesta correcta. (0,5 puntos)

Si el satélite en la órbita alrededor de la Tierra pierde masa en su recorrido, su período de rotación:

1.  se reduce en la misma proporción;

2.  aumenta en esa proporción;

3.  no varía.

 

La respuesta correcta es la 3. Si el satélite en la órbita alrededor de la Tierra pierde masa en su recorrido, su periodo de rotación no varía. El período es el tiempo que el satélite tarda en dar una vuelta completa y lo podemos calcular a partir de la velocidad orbital calculada anteriormente:

 

 

Como vemos en la última expresión, la masa del satélite no influye para nada en su período de rotación.

 

1.3. Responda estos dos apartados. (1 punto)

1.  Calcule el trabajo mínimo que es necesario realizar sobre el satélite para situarlo en la órbita circular geoestacionaria.

 

El trabajo es igual a la diferencia de energía que tiene el satélite en la órbita menos la que tiene en la superficie de la Tierra. Comenzamos calculando la energía potencial que tiene el satélite en la superficie de la Tierra:

 

 

 

En la órbita el satélite va a tener tanto energía cinética como energía potencial, de forma que la energía total o mecánica es igual a la mitad de la energía potencial:

 

 

 

 

 

 

Calculamos:

 

 

 

 

Por último, calculamos el trabajo para situarlo en órbita:

 

 

 

2.  Calcule la velocidad mínima que necesita el satélite para abandonar esa órbita y alejarse definitivamente de la Tierra.

 

Nos pide ahora que calculemos la velocidad de escape desde la órbita. Es decir, que velocidad como mínimo debemos imprimirle al satélite en la órbita para que llegue a un punto, con velocidad nula, lo suficientemente lejos de la Tierra como para que la atracción de esta sea cero (al infinito). La calculamos sabiendo que el campo gravitatorio es un campo de fuerzas conservativo y, por lo tanto, la energía se conserva:

 

 

 

La energía cinética en el infinito es cero porque a ese punto, por definición, llega con velocidad nula. También es cero la energía potencial del infinito, puesto que la distancia entre la Tierra y el satélite es infinita:

 

 

 

 

 

 

DATOS: