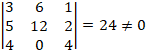Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2024
PREGUNTA 2. Números y Álgebra.
Discuta, según los valores de m, el siguiente sistema:
.png)
Planteamos dos matrices, la de coeficientes (A) y la ampliada con los términos independientes (A*):
.png)
Calculamos el determinante de la matriz A para determinar su rango. I:
.png)
Igualamos a cero el determinante para saber qué valores de m lo anulan:
.png){kind=small}
El rango de la matriz A será:
· Si .png){kind=small}
.
· Si .png){kind=small}
, ya que encontramos algún determinante de este orden distinto de cero:
.png){kind=small}
· Si .png){kind=small}
, ya que encontramos algún determinante de este orden distinto de cero:
.png){kind=small}
Los casos que tenemos entonces serían los siguientes:
· Si 
El rango de la matriz ampliada es 3, porque el determinante de A, que era distinto de cero, también está en la matriz ampliada.
· Si .png){kind=small}
El rango de la matriz ampliada es 3 porque hay algún determinante de este orden distinto de cero:
.png)
· Si 
El rango de la matriz ampliada es 3 porque hay algún determinante de este orden distinto de cero:
|
|
Página 2 de 8 | 
|
|
