Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2023

3. Análisis:

a)  Si  ,  diga  qué  valores  deben  de tener  a  y  b  para  que  se  cumplan   y    .

b) Estudie si la función  tiene extremos relativos o puntos de inflexión en el intervalo , diga donde están en caso de que existan y esboce la gráfica de f en ese intervalo.

 

a)   Calculamos la imagen del cero:

 

 

Hallamos el límite:

 

 

Como sabemos que el numerador es cero, ya que es la imagen de cero de la función, aplicamos L’Hôpital para resolver la indeterminación:

 

 

Como el resultado del límite es 3, obtenemos el valor de a y a continuación el de b:

 

 

 

 

b)  El dominio de la función f(x) es . Para calcular los extremos relativos hacemos la primera derivada y la igualamos a cero:

 

 

 

 

Como buscamos la solución en la primera vuelta nos quedamos con la solución . Hacemos la segunda derivada para comprobar si hay un mínimo, un máximo o nada:

 

 

 

Como vemos la función no tiene extremos relativos, algo que se comprueba fácilmente viendo la primera derivada, ya que siempre va a tomar valores positivos o como mucho cero. Así, la función siempre es creciente y por lo tanto no tiene extremos relativos.

 

Para hallar los puntos de inflexión igualamos a cero la segunda derivada:

 

 

Como nos quedamos con la solución de la primera vuelta, los posibles puntos de inflexión los tenemos en 0⁰ y 180⁰. Comprobamos si lo son o no con la tercera derivada:

 

 

 

 

Calculamos la otra coordenada de estos puntos:

 

 

 

La función f(x) tiene dos puntos de inflexión en los puntos  y .

 

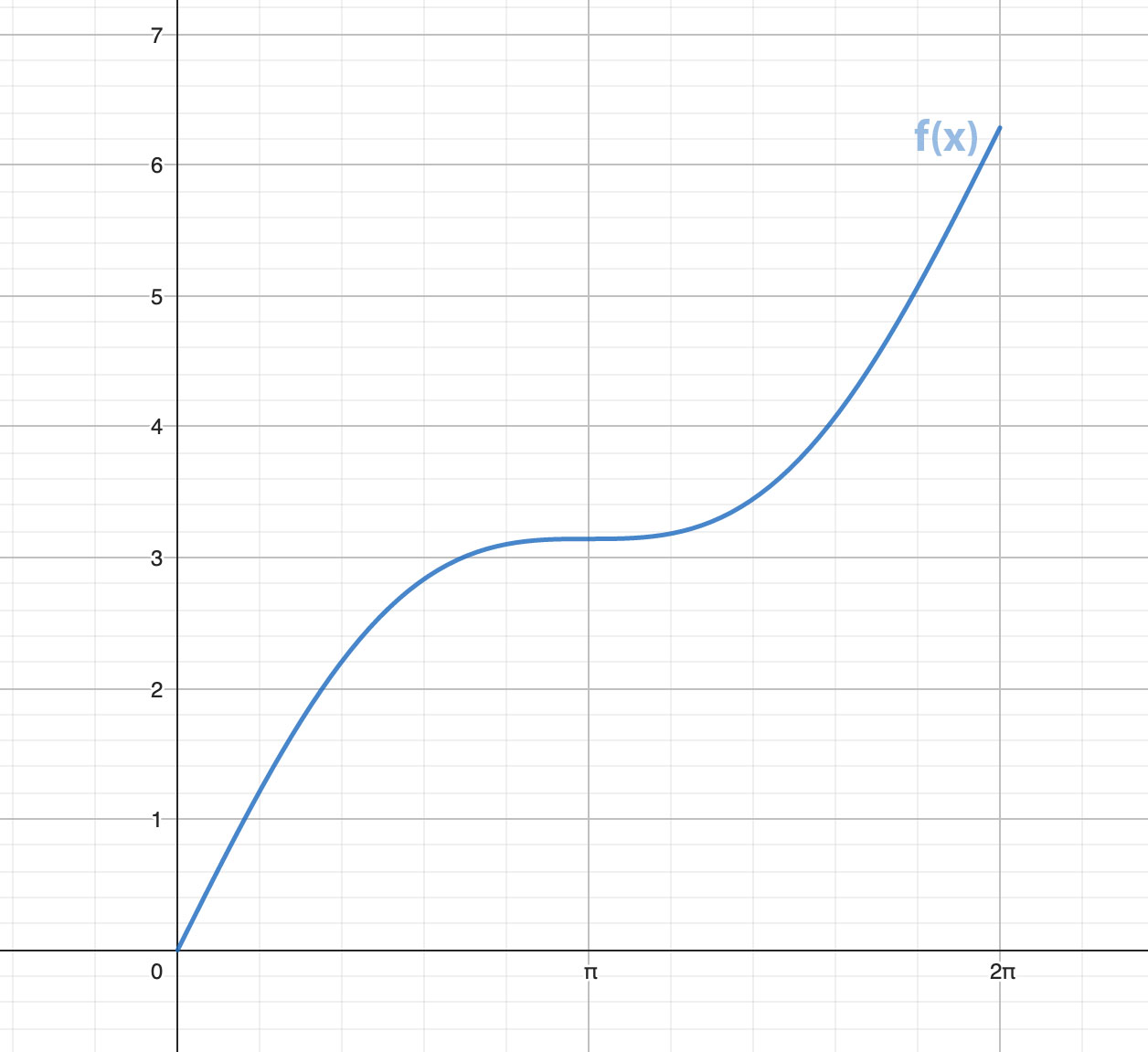
Así entonces, la gráfica sería así: