Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2021

6. Geometría:

a)  Calcule el valor de a si el plano    es paralelo a la recta .

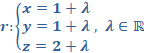b)  Estudie la posición relativa de los planos   y  en función del parámetro m.

a)   Si el plano y la recta son paralelos, el vector normal del plano y el vector director de la recta serán perpendiculares:

b)  Para estudiar la posición relativa de los planos vamos a hacer dos matrices con las ecuaciones de los mismos. En una pondremos los vectores normales y en la otra pondremos también los términos independientes:

Calculamos los rangos de ambas:

·    Si . Si las dos matrices tienen rango 2, significa que los vectores normales no tienen la misma dirección y por lo tanto los planos tampoco. En este caso serían secantes.

·   Si . El rango de la matriz ampliada es 2 porque hay por lo menos una matriz de ese orden con determinante distinto de cero:

El rango de la matriz de los vectores normales es 1, es decir, estos vectores son paralelos, por tanto los planos o bien son también paralelos o coincidentes. Como el rango de la matriz ampliada es 2 significa que no son el mismo plano, es decir, no son coincidentes son paralelos.