Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2021

5. Geometría:

a)  Obtenga la ecuación implícita del plano  que pasa por los puntos ,  y

b)  Calcule el punto simétrico de  con respecto al plano .

a)   Una de las maneras de determinar un plano es a partir de dos vectores y un punto. Por lo que, vamos a hacer dos vectores con los puntos que nos dan:

Con los vectores y uno cualquiera de los puntos calculamos el determinante, igualamos a cero y obtenemos la ecuación implícita del plano:

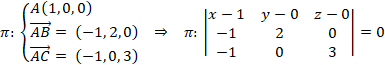
b)  Vamos a calcular una recta r, perpendicular al plano y que pasa por el punto P. Por lo tanto, el vector director de esa recta llevará la misma dirección que el vector normal del plano:

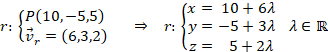
Ahora, calculamos el punto M, punto de corte de la recta y del plano. Para eso sustituimos las ecuaciones paramétricas de la recta en el plano:

Con este valor de , vamos a la recta y calculamos el punto de intersección:

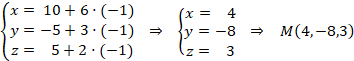
Sabiendo que M es el punto medio de P y P’, podemos calcular el punto simétrico que nos piden: