Galicia. Examen EBAU resuelto de Matemáticas II. Julio 2020

4. Análisis:

a)  Calcule los valores de b y c para que la función    sea, primero continua, y luego derivable en x = 0.

b)  Calcule  .

 

a)   Para  que  una  función  sea  derivable,  debe  ser  continua.  Por  eso vamos a empezar estudiando la continuidad en x = 0:

 

 

 

 

Para que sea continua c debe tomar el valor calculado. Estudiemos ahora la derivabilidad. Como la función es continua en ese punto, puede ser derivable. Lo comprobamos:

 

 

 

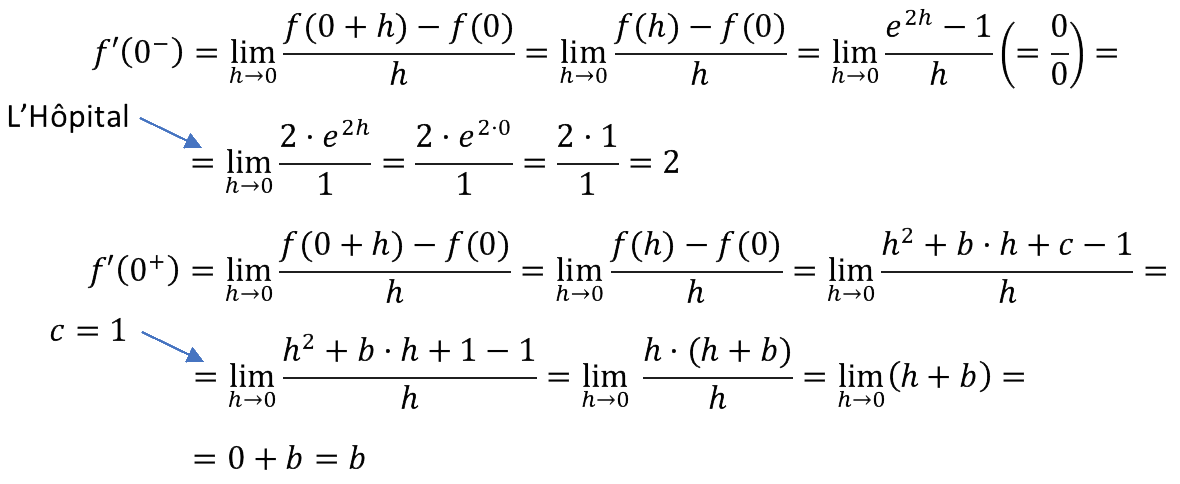
Para ser derivable debe cumplir:

 

 

La función es continua y derivable si    y  .

 

 

b)  Primero vamos a resolver la integral indefinida:

La integral propuesta vamos a resolverla por partes, la fórmula sería:

 

 

 

 

La integral quedaría:

 

 

 

Una vez resuelta la integral definida, vamos a resolver la definida:

 

 

 

El resultado final de la integral sería: