Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Julio 2020

PREGUNTA 2.  Álgebra. Un fabricante de sistemas de iluminación quiere producir focos de tecnología led en dos modelos distintos: A y B. Para diseñar la estrategia de producción diaria tendrá en cuenta que se producirán al menos 50 focos del modelo A, que el número de focos del modelo B no superará las 300 unidades y que se producirán al menos tantos focos del modelo B como del modelo A. Además, la producción total no superará las 500 unidades diarias.

a)  Formule el sistema de inecuaciones asociado al problema.

b)  Representa la región factible y calcule sus vértices.

c)   Si el beneficio obtenido por cada foco del modelo A es de 60 euros y por cada foco del modelo B es de 40 euros, ¿cuántos focos de cada modelo debe producir diariamente para maximizar el beneficio? ¿A cuánto asciende el beneficio máximo?

 

a)   Definimos:

 

x: número de focos del modelo A que produce diariamente.

y: número de focos del modelo B que produce diariamente.

 

Como nos dicen que se producirán al menos 50 focos del modelo A:

 

 

Después dicen que el número de focos del modelo B no superará las 300 unidades:

 

 

Y que se producirán al menos tantos focos del modelo B como del modelo A:

 

 

Por último, la producción total no podrá superar las 500 unidades:

 

 

Todas las restricciones que tenemos que representar serán las siguientes:

 

 

 

 

 

b)  Representamos las restricciones e identificamos la región factible:

 

 

 

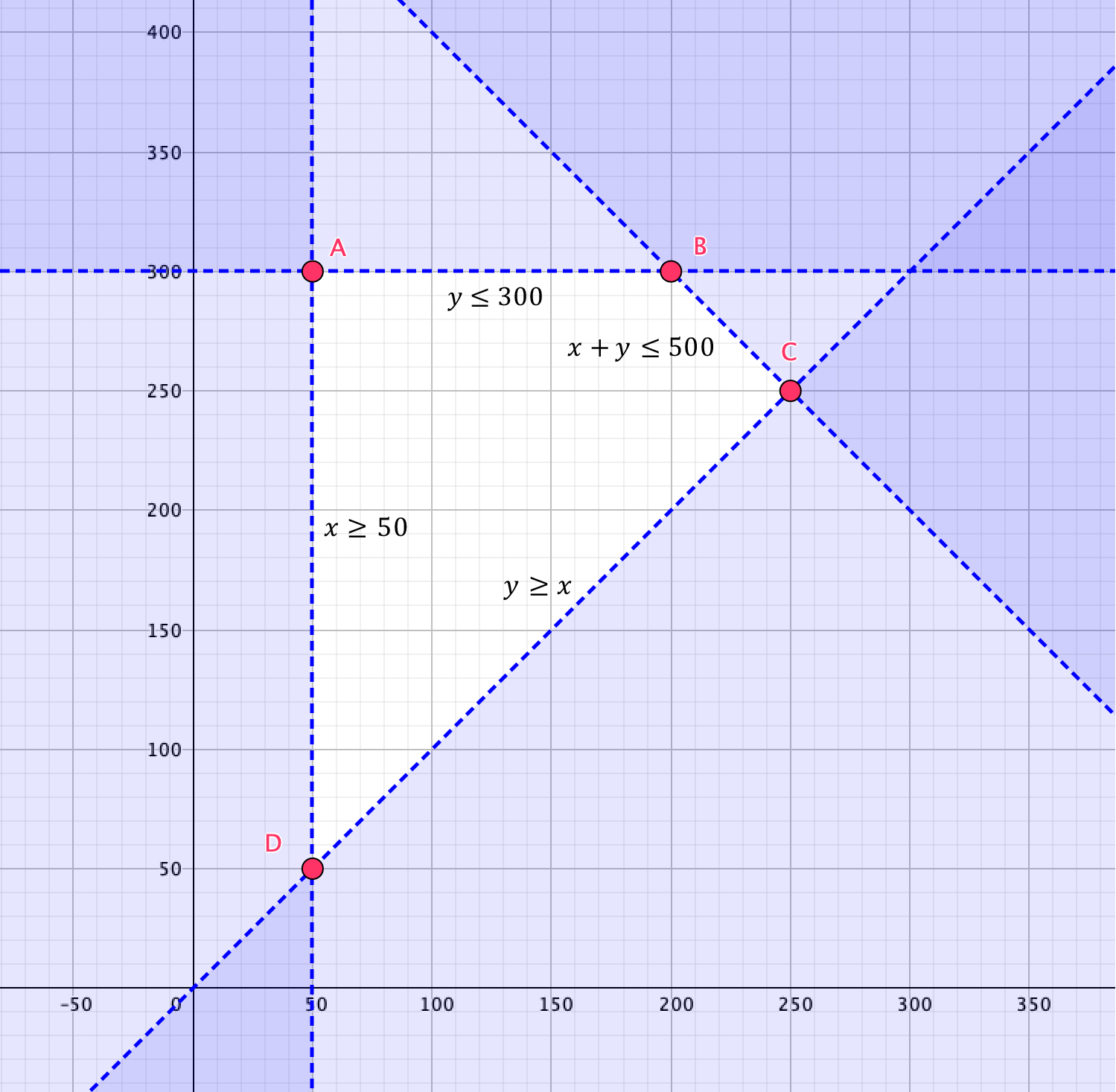
Calculamos los vértices:

 

     ;    

 

       ;    

 

c)   La función de beneficios sería la siguiente:

 

 

Esta función nos dará los beneficios diarios. Calculamos el valor de la misma en cada uno de los vértices de la región factible:

 

 

 

 

 

 

El beneficio máximo diario es de 25 000 euros y se obtiene produciendo 250 focos del modelo A y otros 250 del modelo B.