Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2019

3.   Da respuesta a los apartados siguientes:

a)  Estudia la posición relativa de los planos   y   en función del parámetro m.

b)  Obtén la ecuación implícita del plano que pasa por los puntos ,   y .

c)  Calcula el punto simétrico del punto  con respecto al plano .

 

a)   Para estudiar la posición relativa de los planos vamos a hacer dos matrices con las ecuaciones de los mismos. En una pondremos los vectores normales y en la otra pondremos también los términos independientes:

 

 

Calculamos los rangos de ambas:

 

 

·     Si . Si las dos matrices tienen rango 2, significa que los vectores normales no tienen la misma dirección y por lo tanto los planos tampoco. En este caso serían secantes.

 

·   Si . El rango de la matriz ampliada es 2 porque hay por lo menos una matriz de ese orden con determinante distinto de cero:

 

 

El rango de la matriz de los vectores normales es 1, es decir, estos vectores son paralelos, por lo que los planos o bien son también paralelos o coincidentes. Como el rango de la matriz ampliada es 2 significa que no son el mismo plano, es decir, no son coincidentes son paralelos.

 

b)  Una de las maneras de determinar un plano es a partir de dos vectores y un punto. Por lo que, vamos a hacer dos vectores con los puntos que nos dan:

Con los vectores y uno cualquiera de los puntos calculamos el determinante, igualamos a cero y obtenemos la ecuación implícita del plano: 

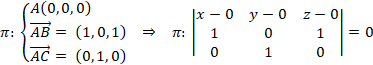
Fijándonos en el plano que nos dan en el último apartado, como es el mismo, le ponemos el mismo nombre.

 

c) 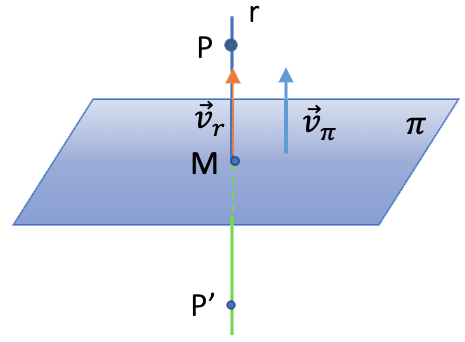 Para calcular el punto simétrico del punto  respecto del plano    vamos a calcular una recta r, perpendicular al plano que pase por el punto P. Por lo tanto, el vector director de esa recta llevará la misma dirección que el vector normal del plano:

 

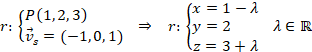
Ahora vamos a calcular el punto M, es decir, el punto donde esta recta corta al plano. Para ello substituimos las ecuaciones paramétricas de la recta en el plano:

 

 

Con el valor del parámetro calculamos el punto sustituyéndolo en las ecuaciones paramétricas de la recta:

 

 

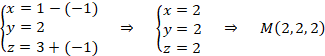
Este punto es el punto medio entre el punto P y su simétrico, P’: