Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2019

2.   Considérese la función . Se pide:

a)  Calcular los límites  y .

b)  Determinar intervalos de crecimiento y decrecimiento, extremos relativos y puntos de inflexión.

c)  Calcular .

 

a)   Vamos a resolver los límites, en el primero de ellos, aplicando dos veces la regla de L’Hôpital para resolver las indeterminaciones. El segundo es inmediato:

 

 

 

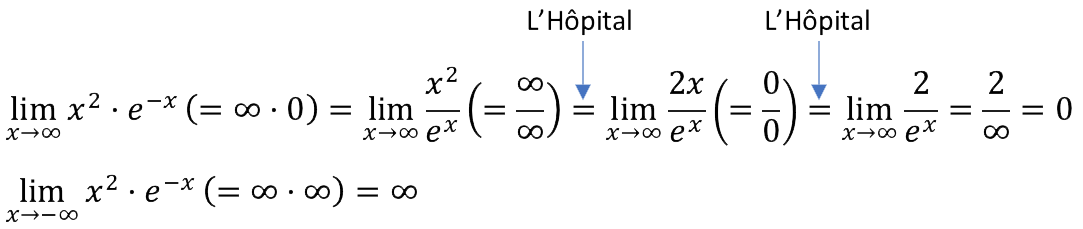
b)  Para calcular los intervalos de crecimiento y decrecimiento hacemos la primera derivada:

Igualamos a cero para calcular los posibles extremos relativos y para obtener los intervalos de crecimiento y decrecimiento:

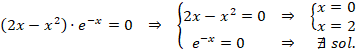
Miramos el signo de la primera derivada en los intervalos obtenidos:

 

f(x) crece en

f(x) decrece en

La función va a tener dos extremos relativos, en x = 0 y en x = 2. Comprobamos, substituyéndolos en la segunda derivada, si son máximos o mínimos:

 

Calculamos las coordenadas y de estos 2 puntos: 

Por último, los puntos de inflexión anulan la segunda derivada, por lo que igualamos esta a cero:

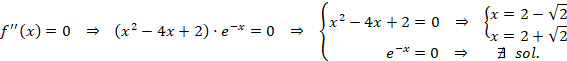
Comprobamos si realmente son puntos de inflexión substituyendo en la tercera derivada:

 

Como vemos al substituirlas en la tercera derivada da distinto de cero, por lo que sí son puntos de inflexión. Calculamos las coordenadas y:

 

c)   Vamos a resolver la integral propuesta:

La integral propuesta vamos a resolverla por partes, a fórmula sería:

La integral quedaría:

 

Esta otra integral que nos queda volvemos a resolverla por partes:

 

Retomamos ahora el resultado que teníamos ya integrado anteriormente y tenemos la solución final: