Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2019

4.   Da respuesta a los apartados siguientes:

a)  El 40% de los habitantes de una cierta comarca tienen camelias, el 35% tienen rosas y el 21% tienen camelias y rosas. Si se elije al azar un habitante de esa comarca, calcular las cinco probabilidades siguientes: de que tenga camelias o rosas; de que no tenga ni camelias ni rosas; de que tenga camelias, sabiendo que tiene rosas; de que tenga rosas, sabiendo que tiene camelias; y de que solamente tenga rosas o solamente tenga camelias.

b)  Si en un auditorio hay 50 personas, ¿cuál es la probabilidad de que por lo menos 2 naciesen en el mes de enero?

 

a)   Definimos los siguientes sucesos y sus probabilidades:

C = “Habitantes de una cierta comarca que tienen camelias”,

R = “Habitantes de una cierta comarca que tienen rosas”,

Nos dicen también que el 21% de los habitantes de cierta comarca tienen camelias y rosas, es decir, nos dan la probabilidad de la intersección: .

Vamos a hacer un diagrama de árbol con los datos del problema. Para eso necesitamos en primer lugar calcular la probabilidad de que tenga rosas sabiendo que tiene camelias, que ya es una de las probabilidades que nos piden:

Ahora calculamos la probabilidad, también condicionada, de que tenga rosas sabiendo que no tiene camelias. Lo hacemos a partir de la probabilidad total de que tenga rosas, que nos la da el enunciado:

Representamos todas estas probabilidades en el diagrama:

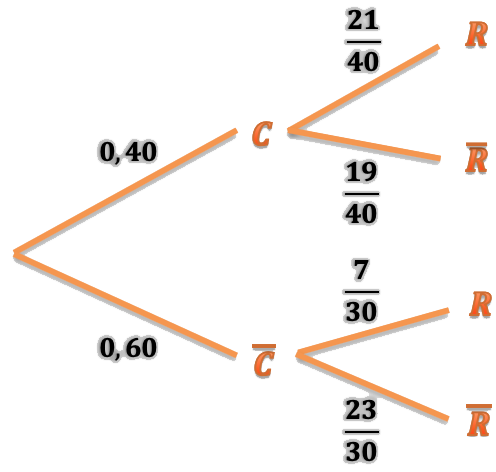
Con los datos del diagrama es fácil calcular todo lo que nos piden. Empezamos por la probabilidad de que tenga camelias o rosas. Es una unión de dos sucesos: 

 

Calculamos la probabilidad de que no tenga ni camelias ni rosas. Esta es la intersección de dos sucesos contrarios o complementarios:

La siguiente es la probabilidad de que tenga camelias sabiendo que tiene rosas. Es una probabilidad condicionada:

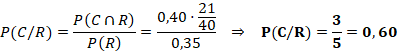
La probabilidad de que sólo tenga rosas será la de que tenga rosas y no camelias:

 

La última que queda es la de que sólo tenga camelias, es decir, que tenga camelias y no rosas:

 

b)  Sea X = “número de personas que nacieron en el mes de enero, de entre las 50”.

La fórmula de la distribución binomial es:

 

La probabilidad que nos piden es:

Calculamos las probabilidades de que el número de personas que nacieron en el mes de enero sea cero o uno:

Calculamos la probabilidad pedida:

La probabilidad de que por lo menos 2 personas nacieran en el mes de enero en un auditorio en el que hay 50 personas es de 0,9285.