Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2019

3.  Se pide: 

a)  Calcular  el  ángulo  del  intervalo  [0⁰, 90⁰]  que  forman  los  vectores   y .

b)  Obtener la ecuación implícita del plano que pasa por el punto  y es perpendicular a la recta:

c)  Calcular la distancia del punto  al plano  y el punto simétrico de Q respecto a .

 

a)   Para calcular o ángulo que forman dos vectores utilizamos el producto escalar:

 

 

Operando queda:

 

 

 

 

 

 

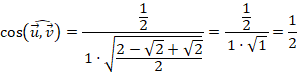
b)  Vamos  a  poner  la  recta  en  las  ecuaciones  paramétricas,  para  eso  vamos  a  pasar  la  z  como  parámetro:

 

 

Así entonces las ecuaciones paramétricas serían:

 

 

De la recta r obtenemos un punto y el vector director:

 

 

Para hacer la ecuación implícita del plano necesitamos un punto del mismo, nos lo dan, es el punto P y el vector normal del mismo, que es el vector director de la recta, pues esta tiene que ser perpendicular a él:

 

 

 

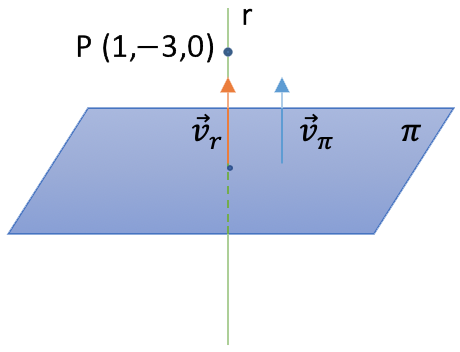
c) 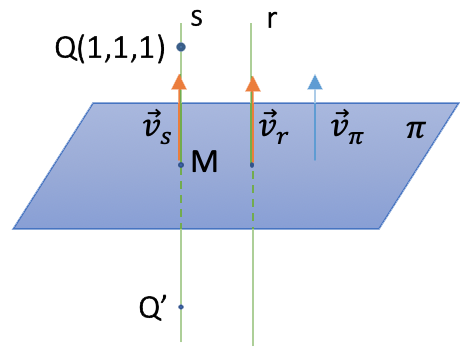  El plano obtenido en el apartado anterior es el que nos dan en este apartado. Ahora tenemos que calcular el punto simétrico de Q con respecto al plano, para eso empezaremos calculando la recta s que pasa por ese punto y es perpendicular al plano, por lo tanto, su vector director es el mismo que el de la recta r y que el del plano :

 

Ahora calcularemos el punto de corte de esta recta con el plano. Para eso substituimos las ecuaciones paramétricas de la recta en la ecuación implícita del plano y obtenemos el valor del parámetro que posteriormente lo substituimos en las ecuaciones de la recta:

 

 

 

Para calcular la distancia del punto Q al plano, sólo tenemos que calcular la distancia entre los puntos Q y M. Lo hacemos haciendo un vector que vaya desde un punto a otro y calculando su módulo:

 

 

 

 

Para calcular el punto simétrico, sabemos que el punto M es el punto medio entre el punto Q y el punto Q’, que es el que buscamos. Utilizando la fórmula del punto medio lo calculamos: