Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2019

2.   Da respuesta a los apartados siguientes:

a)  Mediante  integración  por  partes,  demuestra  que  .  Luego,  demuestra la misma igualdad mediante derivación.

b)  Si ,

 

 

di que relación tiene que existir entre los parámetros a y b para que f sea continua y cuales tienen que ser sus valores para que f sea derivable.

 

 

c)   Calcula   el   área   de   la   región   encerrada   por   el   eje   X,  la  recta  x = 4  y  la  gráfica  de

 

 

a)   Comenzamos, tal y como nos dice el enunciado, resolviendo la integral propuesta por partes:

 

 

 

 

La integral quedaría:

 

 

 

Efectivamente vemos que el resultado de la integral era el que nos daban en el enunciado. Ese resultado es una primitiva de la función, por lo que si la derivamos debemos obtener la función:

 

 

 

Comprobamos que la función obtenida antes era una primitiva, pues al derivarla obtenemos la función original que teníamos antes de derivar.

 

b)  Empezamos estudiando la continuidad. La función  es continua en el intervalo  y la función , por ser polinómica, es continua en . Por lo tanto, el único punto donde puede no serlo es en el que cambiamos de dibujar un trozo a dibujar el otro, es decir en el punto . Para estudiar la continuidad ahí, debe existir el límite en el punto, es decir, que el límite por la izquierda y por la derecha existan y sean iguales y además, el valor del límite debe ser igual al valor que toma la función en ese punto:

 

 

 

Para que f(x) sea continua debe cumplir:

 

 

 

Esta última expresión nos da la relación que tiene que existir entre a y b para que la función sea continua. Estudiamos ahora la derivabilidad, que puede presentar problemas en el mismo punto de antes. Hacemos la derivada por la izquierda y por la derecha:

 

 

 

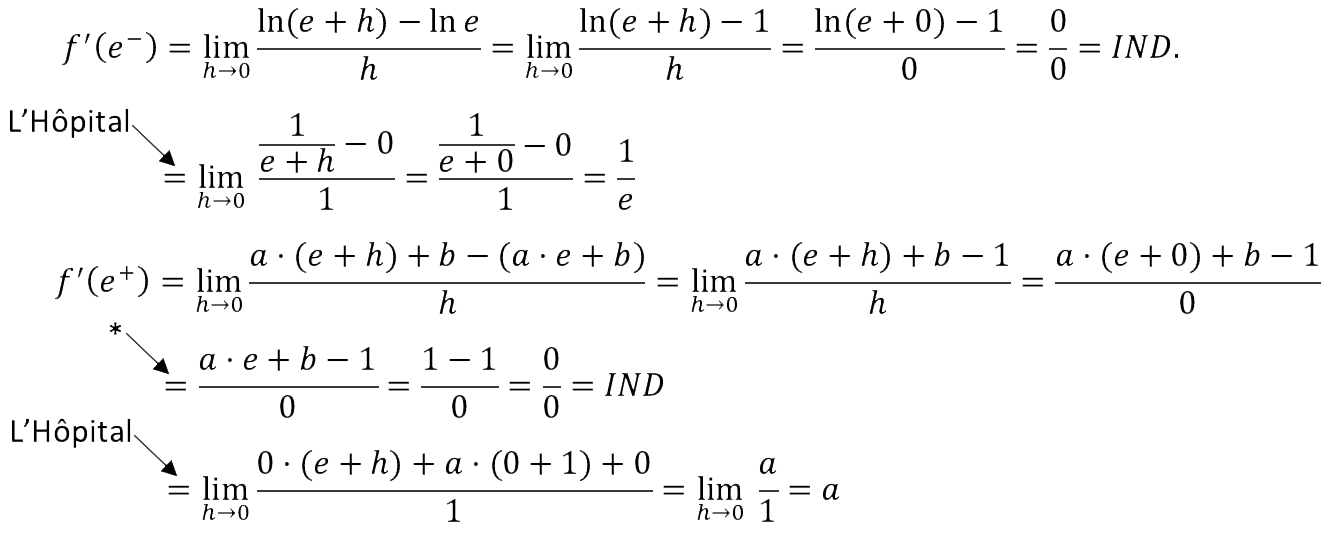
* Aplicamos la condición que debe cumplir la función para ser continua.

Para que sea derivable debe cumplir que las derivadas laterales sean iguales:

 

 

Si vamos a la condición de antes, obtenemos el valor de b:

 

 

c)   Como vemos la función que nos dan en este último apartado es la que se obtendría de substituir los valores calculados en el apartado anterior en la función inicial. Para calcular el área, primero dibujamos los dos trozos de la función y la recta x = 4. Trazamos en ese dibujo una recta vertical que pasa por el punto donde se unen los dos trozos de la función f(x), es decir, la recta x = e:

 

 

 

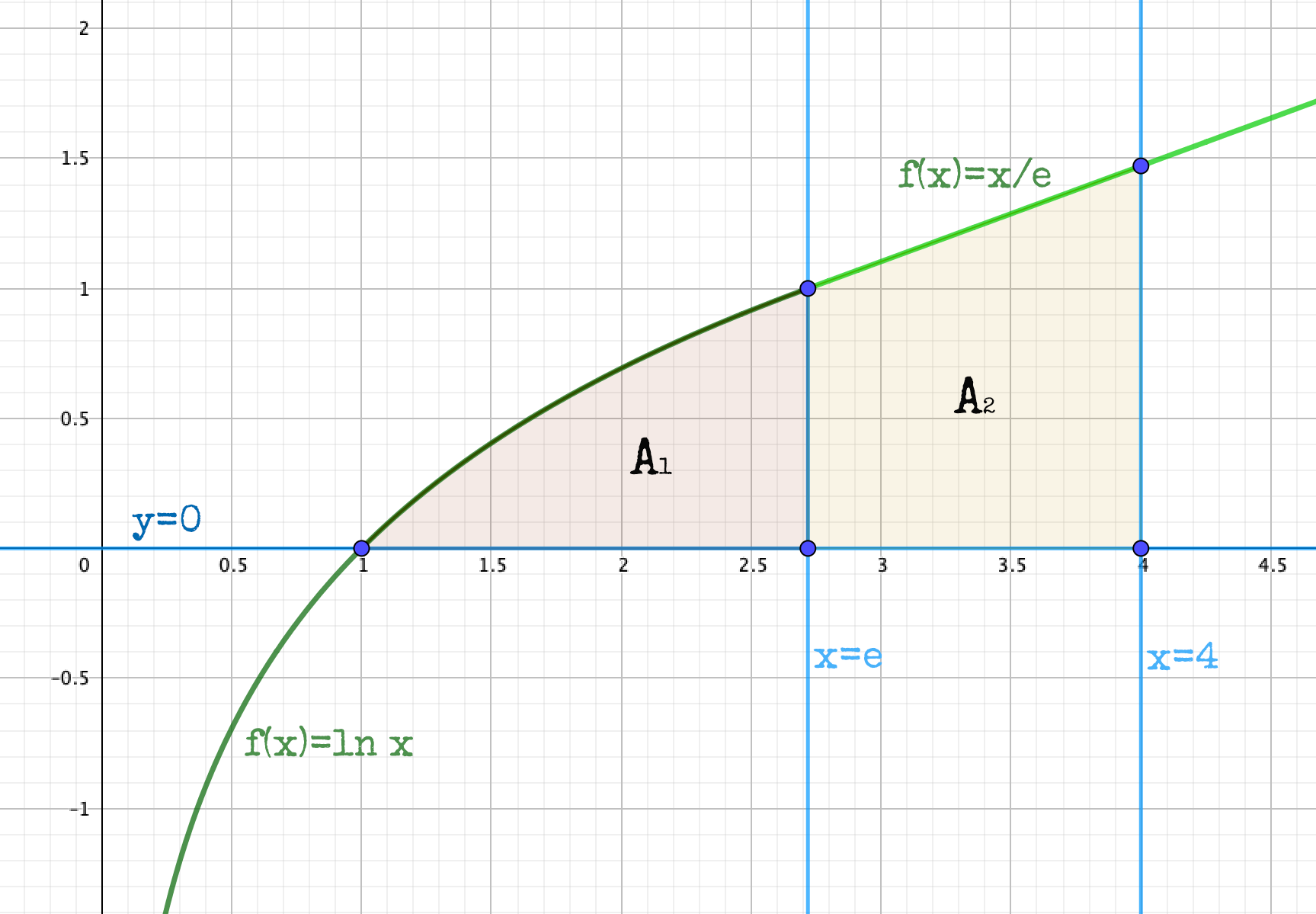
Como vemos tenemos dos áreas, una de ellas A₁ está limitada por la parte superior por el primer trozo de la función y por la parte inferior por el eje OX, es decir la recta y = 0. Calculamos su área sabiendo que la integral la tenemos resuelta en el primer apartado del ejercicio:

 

 

 

La segunda, A₂, está limitada por la parte superior por el otro trozo de la función y por la parte inferior otra vez por el eje OX, y = 0. La calculamos así:

 

 

 

El área que nos piden es la suma de estas dos: