Galicia. Examen EBAU resuelto de Matemáticas II. Septiembre 2018
![]()
3. Sea r la recta que pasa por los puntos ![]() y
y ![]() . Dada la recta
. Dada la recta ![]()
![]()
![]()
![]()
![]()
![]()
a) Estudia la posición relativa de las rectas r y s. Calcula, si se cortan, el punto de corte.
b) Calcula, si existe, la ecuación implícita o general del plano que contiene a las rectas r y s.
c) Calcula la distancia del punto ![]() a la recta s.
a la recta s.
a) Vamos primero a calcular las ecuaciones paramétricas de la recta r:
.png)
La recta s vamos a ponerla también en las ecuaciones paramétricas:
.png)
Los puntos y vectores directores de las dos rectas son:
![]()
Con los puntos de las dos rectas hacemos un vector: ![]() .
.
Ahora en una matriz vamos a poner los dos vectores directores y en otra los dos vectores directores y el vector que hicimos con los puntos de las rectas:
.png)
Calculamos los rangos y sabemos la posición relativa de las rectas:
La matriz A tiene rango 2, ya que: ![]() .
.
Por lo tanto, los vectores directores son linealmente independientes, es decir, no tienen la misma dirección. Por lo que, las rectas sólo pueden ser o secantes o cruzadas.
La matriz A* también tiene rango 2, ya que: .png) .
.
Por lo que el vector que hicimos con los puntos de ambas rectas está en el mismo plano que el de los vectores directores. Por consiguiente, las rectas son secantes.
Ahora, para calcular el punto de corte igualamos las ecuaciones paramétricas de ambas rectas. El sistema resultante es compatible determinado, tiene una solución que es el punto de corte. Para resolverlo, de la última ecuación obtenemos una de las incógnitas y substituyendo en cualquiera de las dos primeras obtenemos el valor de la otra:
.png)
Ahora basta con substituir ![]() en la recta r o
en la recta r o ![]() en la recta s:
en la recta s:
.png)
El punto de corte de r y s es el punto ![]() , justo uno de los puntos que ya nos daba el enunciado.
, justo uno de los puntos que ya nos daba el enunciado.
b) Como vimos en el apartado anterior, las rectas son secantes por lo que, efectivamente podemos obtener la ecuación de un plano que contiene a las dos. Para calcularla utilizamos los vectores directores de ambas rectas y un punto cualquiera de ellas:
.png)
![]()
c) Para calcular la distancia de un punto a una recta utilizamos la fórmula del área de un paralelogramo:
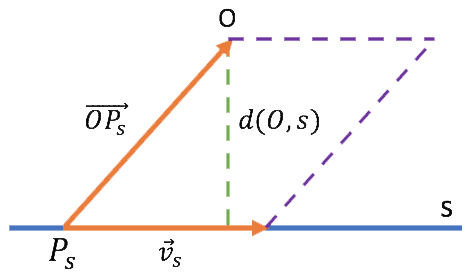
![]()
![]()
![]()
![]()
![]()
.png)
.png)

