Galicia. Examen EBAU resuelto de Matemáticas II. Septiembre 2018

2.    

a)  Calcula, si existe el valor de m para que   .

b)  Calcula  los  valores  de  a,  b,  c  y  d  para  que  la  función    tenga un punto de inflexión en el punto  y la tangente a su gráfica en el punto  sea paralela al eje X.

c)  Calcula  .  (Nota:  logaritmo neperiano)

 

a)   Primero  vamos  a  resolver  el  límite  aplicando  dos  veces la regla de L’Hôpital para resolver las indeterminaciones:

 

 

 

 

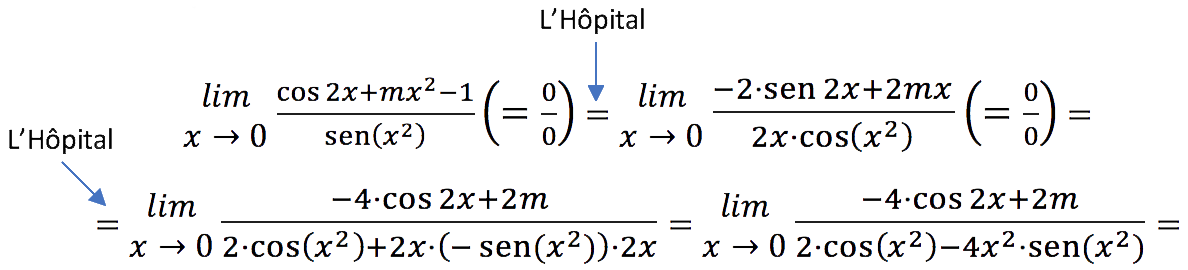
Como nos daban el resultado del límite, igualamos y obtenemos el valor de m:

 

 

 

b)  Para calcular los puntos de inflexión necesitamos hacer la segunda derivada de la función:

 

Como sabemos los puntos de inflexión anulan la segunda derivada, por lo que se cumplirá:

 

Además, el punto de inflexión es un punto de la propia función, por lo que también se verificará que:

 

Una vez calculados estos dos parámetros, la función y la primera derivada nos quedarán así: 

Como nos dice que la tangente a la gráfica en el punto  es paralela al eje X, eso significará que la pendiente de esa recta en ese punto es horizontal, es decir, tendrá pendiente cero. La pendiente de la recta tangente a una función se calcula con la primera derivada, por lo que se cumplirá:

Como ese punto también pertenece a la función tendremos que:

De estas dos últimas condiciones obtenemos sendas ecuaciones. Las juntamos, resolvemos el sistema y obtenemos los valores que nos faltan:

 

c)   Primero vamos a resolver la integral indefinida:

La integral propuesta vamos a resolverla por partes, a fórmula sería:

La integral quedaría:

 

 

 

Después de operar vemos que nos queda otra integral igual que la que ya resolvimos para obtener v, por lo tanto, finalmente nos quedará:

 

 

Una vez resuelta la integral definida, vamos a resolver la definida:

 

 

 

El resultado final de la integral sería: