Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2018

2.    

a)  Calcula a y b para que la función    sea continua y derivable en .

b)  Calcula los vértices del rectángulo de área máxima que se puede construir, si uno de los vértices es el , otro está sobre el eje X, otro sobre el eje Y y el otro sobre la recta  .

c)  Calcula  .

 

a)   Para  que  una  función  sea  derivable,  debe  ser  continua. Por eso vamos a empezar estudiando la continuidad en x = 0:

 

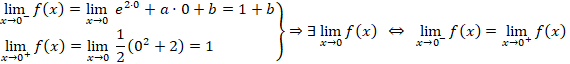
Estudiemos ahora la derivabilidad. Como la función es continua en ese punto, puede ser derivable. Lo comprobamos:

 

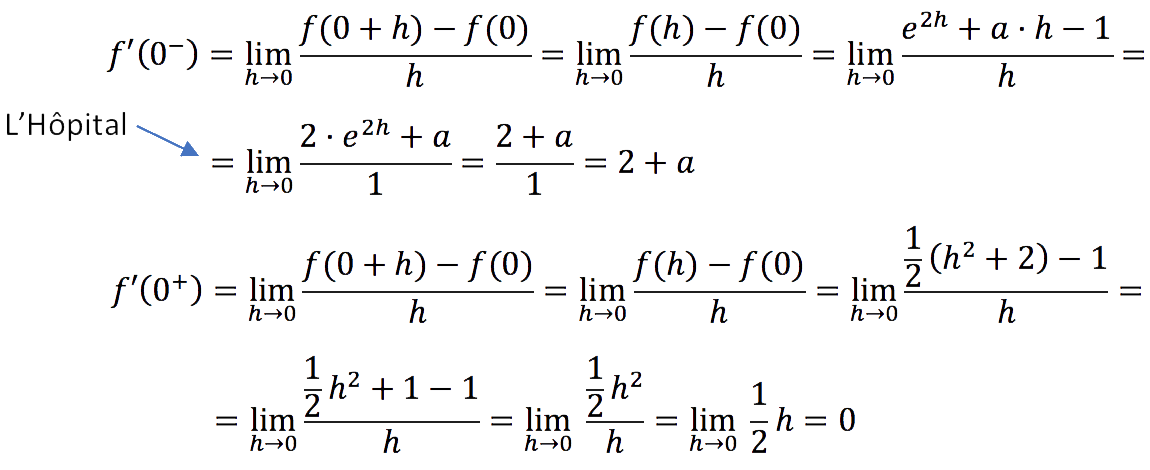
Para ser derivable debe cumplir:

 

 

La función es continua y derivable si    y  .

 

b)  Hacemos un dibujo del rectángulo y de la recta que nos dan:

  

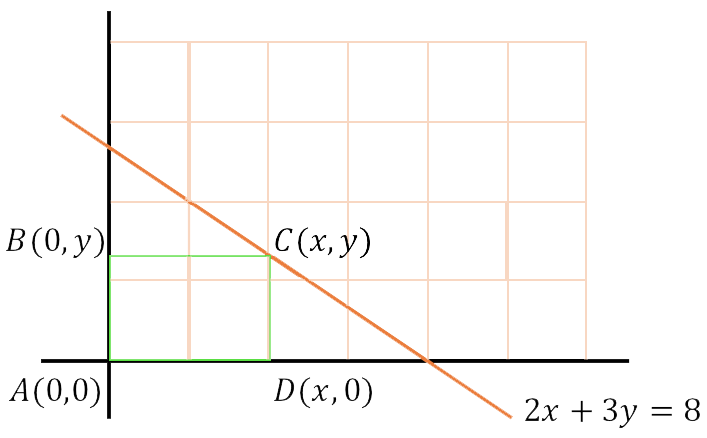
Con los datos que tenemos calculamos el área del rectángulo: 

Con la ecuación de la recta relacionamos la longitud de la base y de la altura para dejar el área en función de una sola variable: 

Para calcular los posibles máximos y mínimos de la función, hacemos la primera derivada e igualamos a cero:

Comprobamos si ese valor hace máxima o mínima el área del rectángulo. Lo hacemos con la segunda derivada:

En la ecuación de la recta calculamos la otra coordenada y ya tenemos todos los vértices del rectángulo que hacen máxima su área: 

 

c)   Primero vamos a resolver la integral indefinida:

La vamos a resolver por cambio de variable. El cambio lo hacemos con la intención de que después del mismo nos quedemos sin la raíz cuadrada:

Necesitamos derivar los dos miembros de la ecuación:

Planteamos y resolvemos la integral con el cambio propuesto:

 

 

Deshacemos el cambio:

 

Por último, resolvemos la integral definida que nos pedían: