Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Junio 2018

2.   El salario diario de un joven durante los cinco primeros años en determinada empresa se ajusta a la siguiente función, donde t representa el tiempo, en años, que lleva contratado:

 

 

a)  Estudia el crecimiento y decrecimiento de la función salario y represéntala.

b)  ¿En qué momento tuvo un salario máximo? ¿Y mínimo? Calcula dichos salarios.

 

a)   Para calcular la monotonía de la función hacemos la primera derivada:

 

 

Igualamos a cero la primera derivada para calcular los puntos críticos:

 

 

Teniendo en cuenta el dominio de la función  y el posible extremo relativo, estudiamos el crecimiento de la función mirando el signo que toma la primera derivada:

 

 

 

Por lo tanto, el salario se mantuvo estable el primer año, aumentó entre el primer y el cuarto año y disminuyó del cuarto al quinto año.

 

Como vemos la función tiene un máximo en el cuarto año, ya que antes la función crece y después decrece. Para representar vamos a calcular qué valor toma la función en ese máximo y en todos los años intermedios:

 

 

 

 

 

 

Hacemos la representación gráfica:

 

 

 

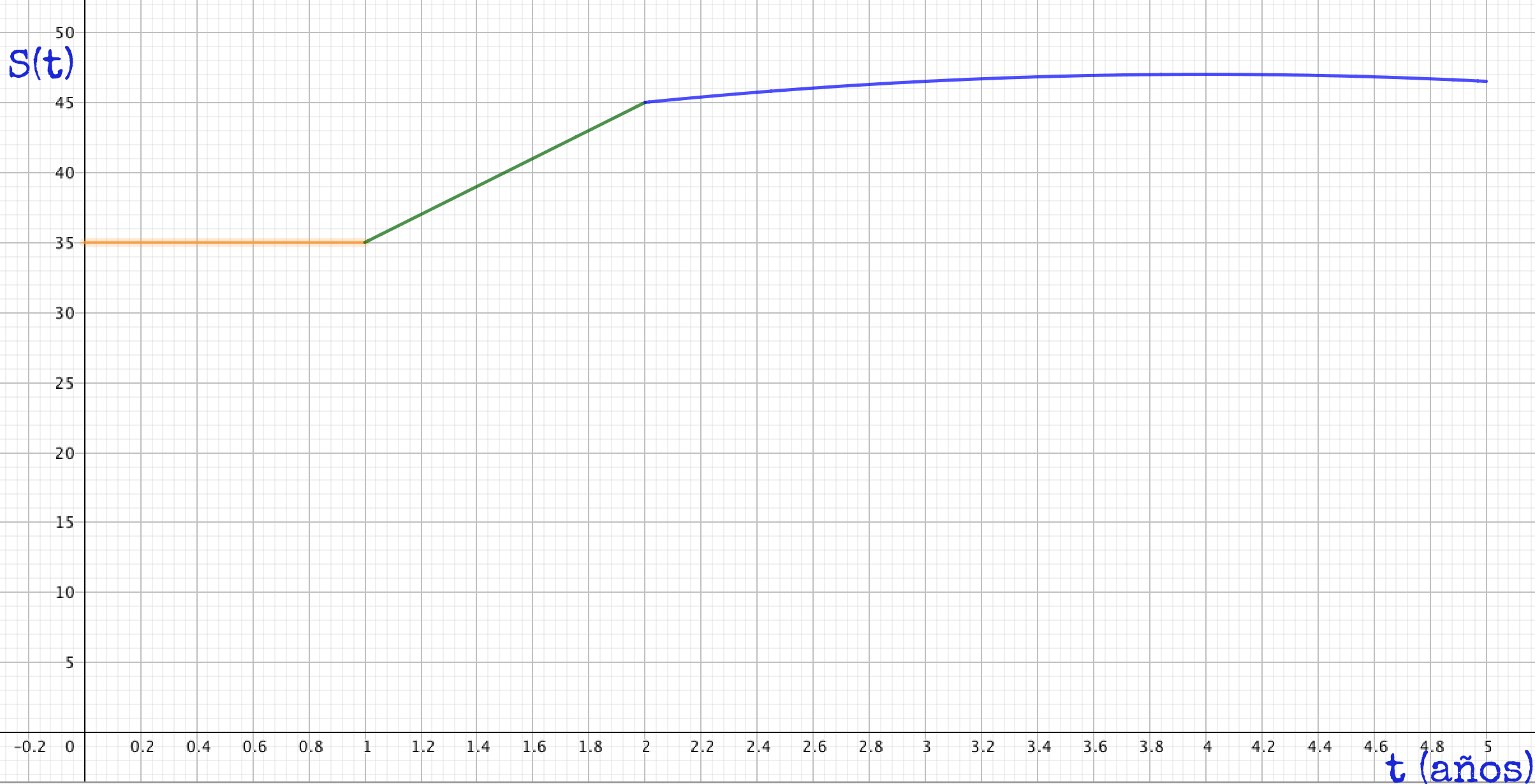
b)  Con los cálculos que hicimos en el apartado anterior ya tenemos la respuesta a lo que nos preguntan:

 

El salario máximo lo tuvo a los 4 años y fue de 47 (no se pueden poner unidades porque el enunciado no nos dice si son euros, miles de euros…). El salario mínimo lo tuvo a lo largo del primer año y fue de 35.