Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Junio 2018

1.   Una  pastelería  hace  con  harina  y  nata  dos   tipos   de  bizcochos:  suave  y  duro.   Dispone   de  160 quilogramos de harina y 100 quilogramos de nata. Para fabricar un bizcocho suave necesita 250 gramos de harina y 250 gramos de nata y para fabricar un bizcocho duro necesita 400 gramos de harina y 100 gramos de nata. Además, el número de bizcochos suaves fabricados debe exceder al menos en 100 unidades al número de bizcochos duros. Si los bizcochos suaves se venden a 6 € y los bizcochos duros a 4,5 €,

a)  Formula un problema que controle la fabricación de bizcochos maximizando las ventas.

b)  Representa la región factible.

c)   ¿Qué   cantidad   se   debe  fabricar  de  cada  tipo  para  maximizar  dichas  ventas?   ¿A  cuánto ascienden?

 

a)   Definimos:

 

x: número de bizcochos suaves que fabrica la pastelería.

y: número de bizcochos duros que fabrica la pastelería.

 

Los quilogramos de harina que se gastan en cada tipo de bizcochos tienen que ser igual o menor a los quilogramos de los que se dispone:

 

 

Sucede lo mismo con los quilogramos de nata:

 

 

Tenemos otra restricción debida a que el número de bizcochos suaves debe exceder al menos en 100 unidades al número de bizcochos duros:

 

 

Por lógica, tanto el número de bizcochos suaves como duros debe ser mayor o igual a cero. Pero como veremos en el apartado siguiente, cuando hagamos la representación de las restricciones, sólo necesitamos una de las dos:

 

 

Nos queda la función a maximizar. Sería:

 

 

b)  Calculamos los vértices:

 

  ⇒    ;       ⇒     

 

   ⇒    ;     ⇒     

 

 

 

Como x e y son número de bizcochos, el vértice B tiene que tener de coordenadas números enteros, por lo que redondearemos. Si redondeamos los dos valores al alza, no nos llegaría la harina, pero si redondeamos la primera coordenada al alza y la segunda a la baja, se siguen cumpliendo las dos restricciones. Por lo que el vértice B sería . Representamos la región factible:

 

 

 

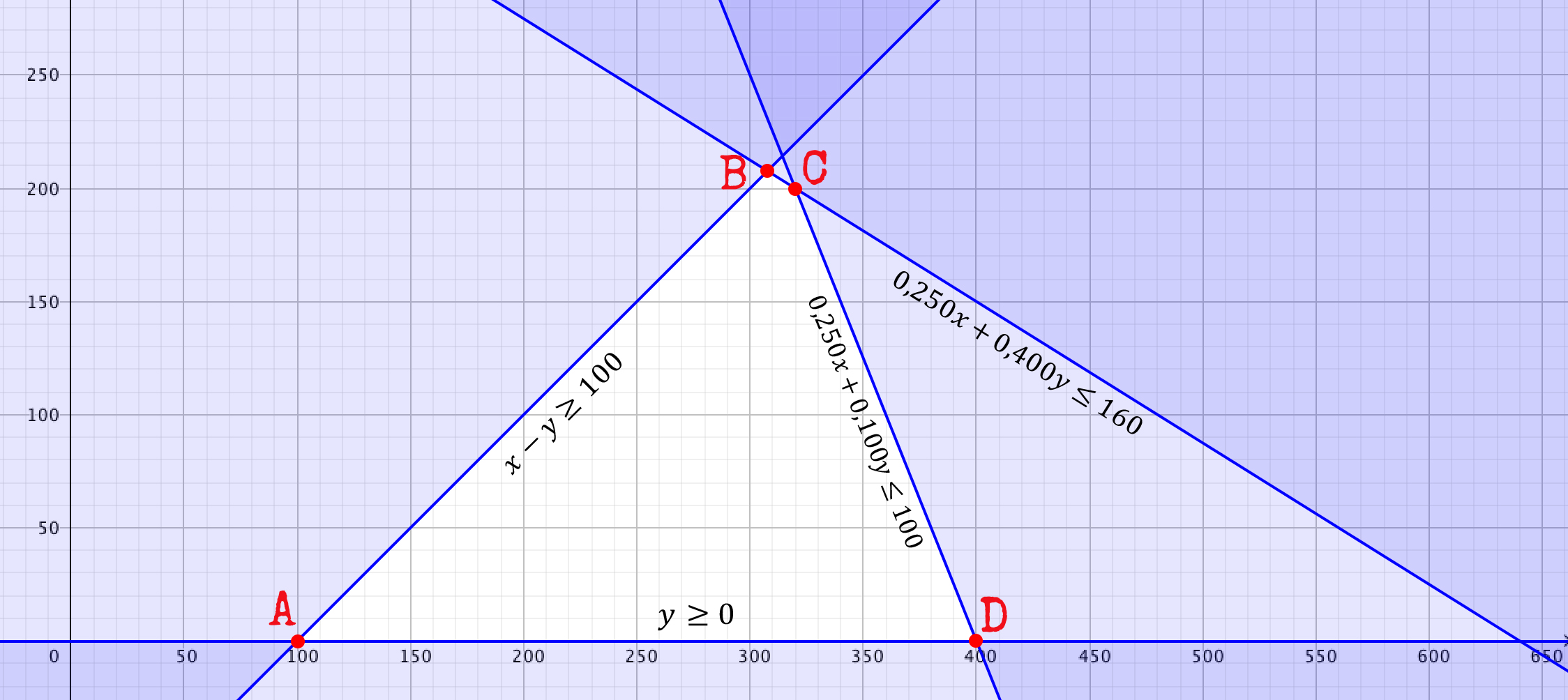
c)   Calculamos en que vértice toma la función ingresos el valor máximo:

 

A ⇒

B ⇒

C ⇒   ⇒  Alcanza el máximo

D ⇒

 

Para maximizar las ventas se deben fabricar 320 bizcochos suaves y 200 bizcochos duros. Con ese número de bizcochos se obtendrían unos ingresos de 2 820 €.