Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2017

3.   Sea r la recta que pasa por los puntos  y .

a)   Calcula la distancia del punto  a la recta r.

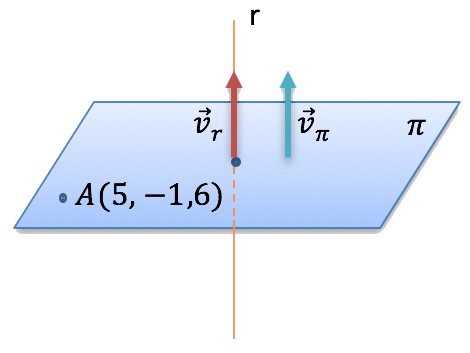
b)  Calcula la ecuación implícita o general del plano que es perpendicular a r y pasa por el punto .

c)   Calcula el área del triángulo de vértices los puntos ,  y el punto de corte de la recta r con el plano .

 

a)  Vamos primero a calcular las ecuaciones paramétricas de la recta:

 

 

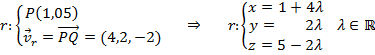
Utilizamos la fórmula para calcular la distancia que nos piden:

 

 

 

 

 

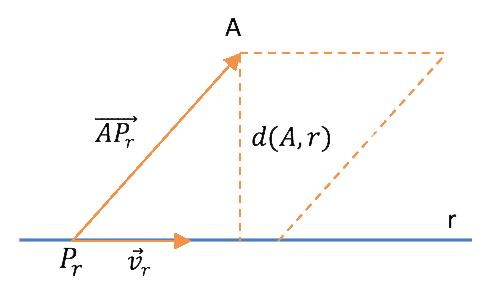
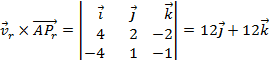
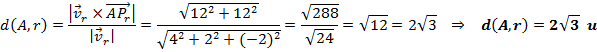
b)  Para calcular el plano tenemos un punto del mismo, el punto A, y como vector normal podemos usar el vector director de la recta, puesto que tiene la misma dirección:

 

 

 

 

 

 

 

      Podemos simplificar la ecuación del plano y nos quedaría:

 

 

 

c)   Primero, vamos a calcular el punto de corte de la recta con el plano, para ello sólo tenemos que sustituir las ecuaciones paramétricas de la recta en el plano:

 

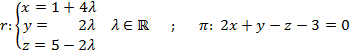
Con el valor del parámetro, vamos a la recta y calculamos el punto de corte:

 

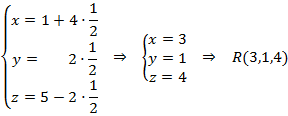
Para calcular el área del triángulo formado por tres vértices, hacemos dos vectores:

 

 

 

El módulo del producto vectorial de estos dos vectores nos daría el área del paralelogramo formado por los vectores. El área del triángulo sería la mitad:
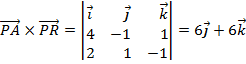