Galicia. Examen EBAU resuelto de Matemáticas II. Septiembre 2017

2.   Dada la función  

 

 

a)  Estudia, en x = 0, la continuidad y derivabilidad de f(x).

 

b)  Determina los puntos de la gráfica de f(x) en los que la recta tangente es paralela a la recta  y determina las ecuaciones de esas rectas tangentes.

c)   Calcula .

 

a)  Primero, vamos a poner la función como una función definida a trozos:

 

 

Para que una función sea derivable, debe ser continua. Por eso vamos a empezar estudiando la continuidad en x = 0:

 

 

 

La función es continua en x = 0, ya que el valor de la función en el punto es igual al límite:

 

 

Estudiemos ahora la derivabilidad. Como la función es continua en ese punto, puede ser derivable. Lo comprobamos:

 

 

 

 

 

Como las derivadas laterales en el punto son iguales, la función también es derivable en ese punto, en x = 0:

 

 

b)  Para determinar el punto o los puntos de la función en que la recta tangente es paralela a la recta que nos dan, debemos determinar primero la pendiente de esta:

 

 

Como la pendiente de la recta tangente se calcula con la primera derivada de la función, hacemos la derivada:

 

 

Para que dos rectas sean paralelas deben tener la misma pendiente, por lo que, igualamos la derivada a la pendiente de la recta que nos daban para calcular los puntos de la función que tienen una recta tangente paralela:

 

 

De los cuatro valores obtenidos, dos de ellos no nos valen:

 

 

 

Vamos a determinar la otra coordenada de los otros puntos:

 

 

 

Con todo lo calculado, podemos escribir las dos ecuaciones de las rectas tangentes:

 

 

 

 

 

 

 

c)   Como la integral definida que tenemos que calcular lo tenemos que hacer en el intervalo , lo haremos utilizando el primer trozo de la función:

 

 

Llegamos a una integral racional en la que el numerador es de igual grado que el denominador, por lo que podemos dividir:

 

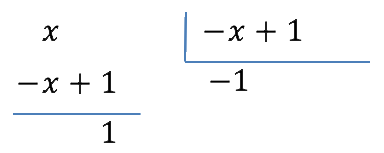Aplicando la regla de la división:

 

 

 

Por lo tanto, la integral nos quedará:

 

 

 

 

El resultado de la integral que nos piden es: