Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2017

2.    

a)  Calcula los valores a, b para que la función   sea derivable en  y determina el punto en el que la tangente a la gráfica de f(x) es paralela a la recta .

 

b)  Si P(x) es un polinomio de tercer grado, con un punto de inflexión en el punto (0,5) y un extremo relativo en el punto (1,1), calcula .

 

a)  Para que una función sea derivable, debe ser continua. Por eso vamos a empezar estudiando la continuidad:

 

La función f(x) es una función continua desde  porque las funciones polinómicas lo son. Lo mismo ocurre de  porque también lo es la función logarítmica. Vamos a estudiar lo que sucede en :

 

 

 

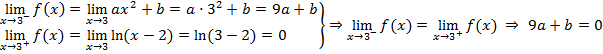
Para que sea continua la función debe cumplir la siguiente condición:

 

 

Estudiemos ahora la derivabilidad. Al igual que la continuidad, la función es derivable en todos los puntos excepto en , porque los dos trozos son funciones derivables. Vamos a mirar lo que sucede en ese punto:

 

 

 

 

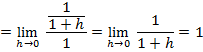
En la derivada lateral por la izquierda, tenemos en cuenta que , porque era la condición que teníamos de la continuidad. En la derivada lateral por la derecha, resolvemos la indeterminación aplicando la regla de L’Hôpital. Así entonces, para que la función sea derivable debe cumplirse:

Si nos vamos ahora a la condición que teníamos de la continuidad, podemos calcular el valor del parámetro que nos falta:

La función nos quedará así:

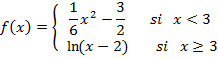
Para determinar el punto de la función en que la recta tangente es paralela a la recta que nos dan, debemos determinar primero la pendiente de esta:

 

Como la pendiente de la recta tangente se calcula con la primera derivada de la función, hacemos la derivada:

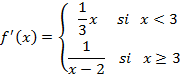
Ahora igualamos la derivada a la pendiente para calcular los puntos de esta que tienen una recta tangente con ese valor:

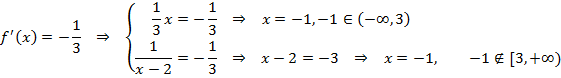
Vamos a determinar la otra coordenada del punto:

Por  lo  que  el  punto  en  el  que  la  recta  tangente  a  la  función  es  paralela  a  la  recta  es .

 

b)  De forma genérica un polinomio de tercer grado sería:  . Para calcular los parámetros debemos calcular la primera y la segunda derivada:

 

Como sabemos que tiene un punto de inflexión en el punto (0,5), este punto debe pertenecer a la función:

La abscisa del punto de inflexión anula la segunda derivada:

Como tiene un extremo relativo en el punto (1,1), este también debe ser un punto de la función:

La abscisa del extremo relativo anula la primera derivada:

Resolvemos el sistema formado por estas dos ecuaciones y calculamos los parámetros que faltan:

 

El polinomio de tercer grado que buscábamos es:

Por último, calculamos la integral que nos piden:
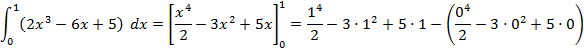