Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2017

1.   Dada la matriz :

a)  Determina, según los valores de , el rango de la matriz , siendo  la matriz traspuesta de A e I la matriz unidad de orden 2.

b)  Determina la matriz  que verifica la ecuación matricial .

a)  Empezamos calculando la matriz :

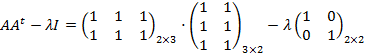
Calculamos el determinante y lo igualamos a cero para saber que valores lo anulan:

Ahora simplemente debemos recordar que el rango de una matriz es igual al orden del mayor determinante distinto de cero, por lo que tendríamos los siguientes casos:

·    Si  .

·    Si  .

b)  Para determinar la matriz pedida, vamos a poner la ecuación en forma matricial y operar:

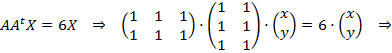
Llegamos a un sistema compatible indeterminado, puesto que las dos ecuaciones son equivalentes. Podemos eliminar una de ellas y en la otra parametrizar una variable:

La matriz que nos piden será: