Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Junio 2017
![]()
1. Consideremos las matrices .png) ,
, .png) ,
, ![]() .
.
(a) Calcula los valores de x e y para los que se satisface la igualdad ![]() .
.
(b) Determina el rango de las matrices A y B.
(c) Calcula X en la ecuación matricial ![]() ,
, ![]() matriz traspuesta de A e I matriz identidad de orden 3.
matriz traspuesta de A e I matriz identidad de orden 3.
(a) Primero, operamos las matrices de la igualdad:
![]()
![]()
Para que dos matrices sean iguales, lo deben ser cada uno de sus elementos:
.png)
(b) Vamos a calcular el rango de las matrices por el método de Gauss:
.png)
Nos quedan tres filas con algún elemento distinto de cero, por lo que el ![]() , es decir, tiene 3 filas y 3 columnas linealmente independientes.
, es decir, tiene 3 filas y 3 columnas linealmente independientes.
.png)
Al final nos quedan dos filas con algún elemento distinto de cero, por lo que el ![]() , es decir, tiene 2 filas y 2 columnas linealmente independientes.
, es decir, tiene 2 filas y 2 columnas linealmente independientes.
(c) Despejamos la matriz a calcular:
![]()
Operamos y calculamos la matriz X, teniendo en cuenta que la matriz traspuesta es la que resulta de cambiar las filar por las columnas:
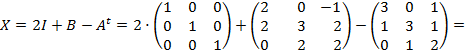
.png)
La matriz que nos piden es:
.png)

