Galicia. Examen PAU resuelto de Matemáticas II. Junio 2016

3.    

a)  Enunciado e interpretación geométrica del teorema de Rolle.

b)  Sea   . Calcula la ecuación de la recta tangente a la gráfica de  en el punto correspondiente a . Determina, si existen, los máximos y mínimos relativos de .

 

a)  El enunciado del teorema de Rolle nos dice:

Sea  f(x)  una  función  continua  en  [a,b], derivable en (a,b) y con f(a) = f(b), entonces existe al menos un  tal que .

 

La interpretación geométrica del teorema es:

 

 

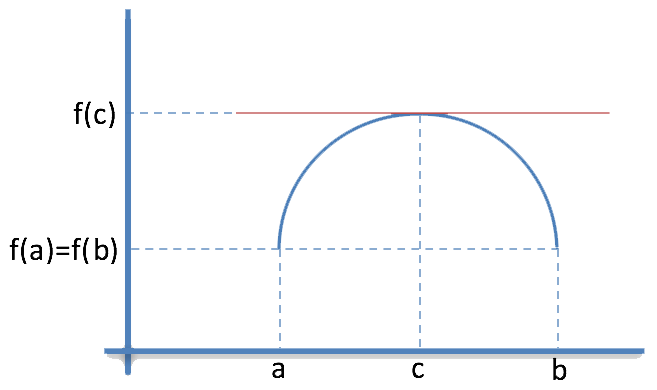
El teorema de Rolle nos dice, que si la función cumple las condiciones, hay al menos un punto donde la recta tangente a la función es paralela al eje OX, ese punto o puntos es donde la derivada se va a anular, es decir, que va a tener por lo menos algún máximo o mínimo en ese intervalo.

 

 

b)  Para calcular la ecuación de la recta tangente a la gráfica necesitamos la primera derivada:

 

 

La pendiente nos la da la derivada de la función en la abscisa del punto de tangencia, es decir, en este caso:

 

 

También necesitamos la otra coordenada del punto de tangencia. Como ese es un punto tanto de la recta tangente como de la función, podremos calcularlo substituyendo en esta última:

 

 

Así entonces, tenemos el punto de tangencia (0,0) y la pendiente . Con lo que utilizando la ecuación punto-pendiente, tenemos la recta que nos piden.

 

 

 

Para calcular los máximos y mínimos relativos tenemos que igualar la primera derivada a cero:

 

Eses dos valores son los posibles extremos relativos, para comprobarlo hacemos la segunda derivada:

 

 

Sustituimos los posibles extremos en la segunda derivada:

 

 

 

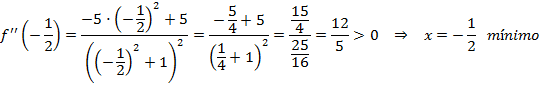
Calculamos la otra coordenada del mínimo y del máximo:

 

 

 

La función tiene dos extremos relativos, que son: