Galicia. Examen PAU resuelto de Matemáticas II. Junio 2016

1.    

a)  Discute, según los valores del parámetro m, el sistema:

 

 

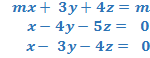
b)  Resuélvelo cuando    y cuando  .

 

a)  Planteamos dos matrices, la de coeficientes (A) y la ampliada con los términos independientes (A^*):

 

 

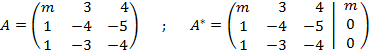
Calculamos el determinante de la matriz A y lo igualamos a cero para saber qué valores anulan dicho determinante y poder así discutir los rangos:

 

 

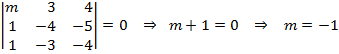
Los casos que tenemos son:

 

·    Si 

 

·    Si  ,  ya que  .

 

Pero la A^* va a tener rango 3, porque si por ejemplo cambiamos la tercera columna de coeficientes por los términos independientes, nos queda:

 

 

 

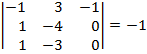
En resumen:

 

 

b)  Para el caso de m = 0, el sistema quedará de la siguiente manera:

 

 

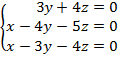
Podemos comprobar que es un sistema homogéneo (los términos independientes son todos nulos). Estos sistemas tienen siempre la solución trivial y como es compatible determinado sólo tiene una solución, que por lo tanto es esa:

 

 

Para m = 1 el sistema quedaría:

 

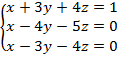
También es compatible determinado, tiene una única solución, y la vamos a calcular utilizando la regla de Cramer:

 

 

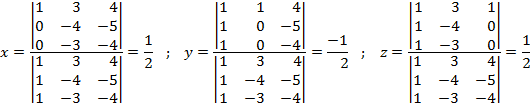
La solución será: