Galicia. Examen PAU resuelto de Matemáticas II. Junio 2016

3.    

a)        Definición e interpretación geométrica del teorema del valor medio del cálculo diferencial.

b)        Calcula los límites siguientes:

i)                                                       ii)   

 

 

a)         El teorema del valor medio del cálculo diferencial sería:

 

Sea  f(x)  una  función  continua  en  [a,b] y derivable en (a,b), entonces existe al menos un  tal que   .

 

 

La interpretación geométrica sería la siguiente:

 

 

 

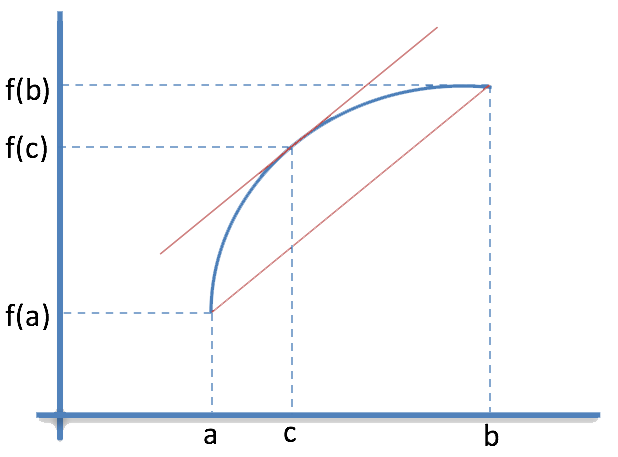
El teorema nos dice, que por lo menos, hay un punto c en el intervalo (a,b) en el que la pendiente de la recta tangente es igual a la pendiente de la cuerda que une los puntos  y . Es decir, que hay una recta tangente en ese punto paralela a dicha cuerda.

 

 

 

 

 

b)       Resolvemos los límites:

 

               i.    Al   substituir   nos   va   a   quedar   una   indeterminación   que   resolveremos   aplicando   la   regla   de L’Hôpital:

        

 

 

 

 

 

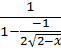
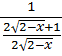
Por lo tanto el límite que nos piden da:

 

  

 

 

              ii.    Igual que el anterior tendremos la misma indeterminación y resolvemos de la misma manera:

      

     

    

 

 

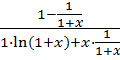
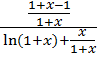
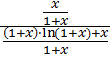
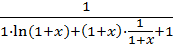
Entonces el límite da: