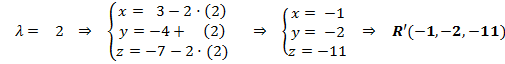Galicia. Examen PAU resuelto de Matemáticas II. Junio 2016

2.    

a)  Calcula el valor de m para que los puntos ,  ,   y   estén en un mismo plano. Calcula la ecuación implícita o general de ese plano.

b)  Calcula el ángulo que forman el plano    y la recta r que pasa por los puntos    y  .

c)   Calcula los puntos de la recta r del apartado anterior que distan 9 unidades del plano .

a)  Empezamos calculando un plano con los puntos B, C y D. Para ello, primero calculamos dos vectores de ese plano:

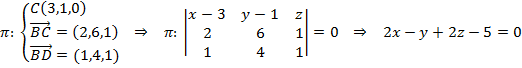
Para que el punto A pertenezca a este plano, debe cumplir la ecuación del mismo:

Para  el punto A está en el formado por los otros puntos y la ecuación implícita de ese plano es  .

b)  Para calcular el ángulo que forma un plano y una recta necesitamos el vector  normal  del  plano,  que lo sacamos  de  la  ecuación  general  del  mismo,  sería:  y  el  vector  director  de  la  recta,  que  será:  . Como podemos ver, son dos vectores proporcionales, tienen la misma dirección, por lo tanto, la recta y el plano serán perpendiculares. Así entonces, r y  son secantes.

c)   Vamos a calcular las ecuaciones paramétricas de la recta r:

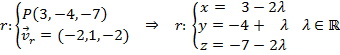
Ahora cogeremos un punto genérico de esa recta  y haremos que la distancia de ese punto al plano sea igual 9 unidades:

Resolvemos:

Para calcular los puntos que distan 9 unidades del plano, sólo debemos substituir los valores del parámetro en la recta r: