Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Junio 2016

1)  Sea la función    sujeta al conjunto de restricciones  ,  ,  ,  .

(a)    Representa gráficamente la región factible y calcula sus vértices.

(b)    Calcula el punto o puntos donde la función alcanza su valor máximo y su valor mínimo. Razona si se obtiene el mismo valor máximo si añadimos la restricción    al conjunto de restricciones anteriores.

 

(a)    La representación gráfica sería esta:

 

 

 

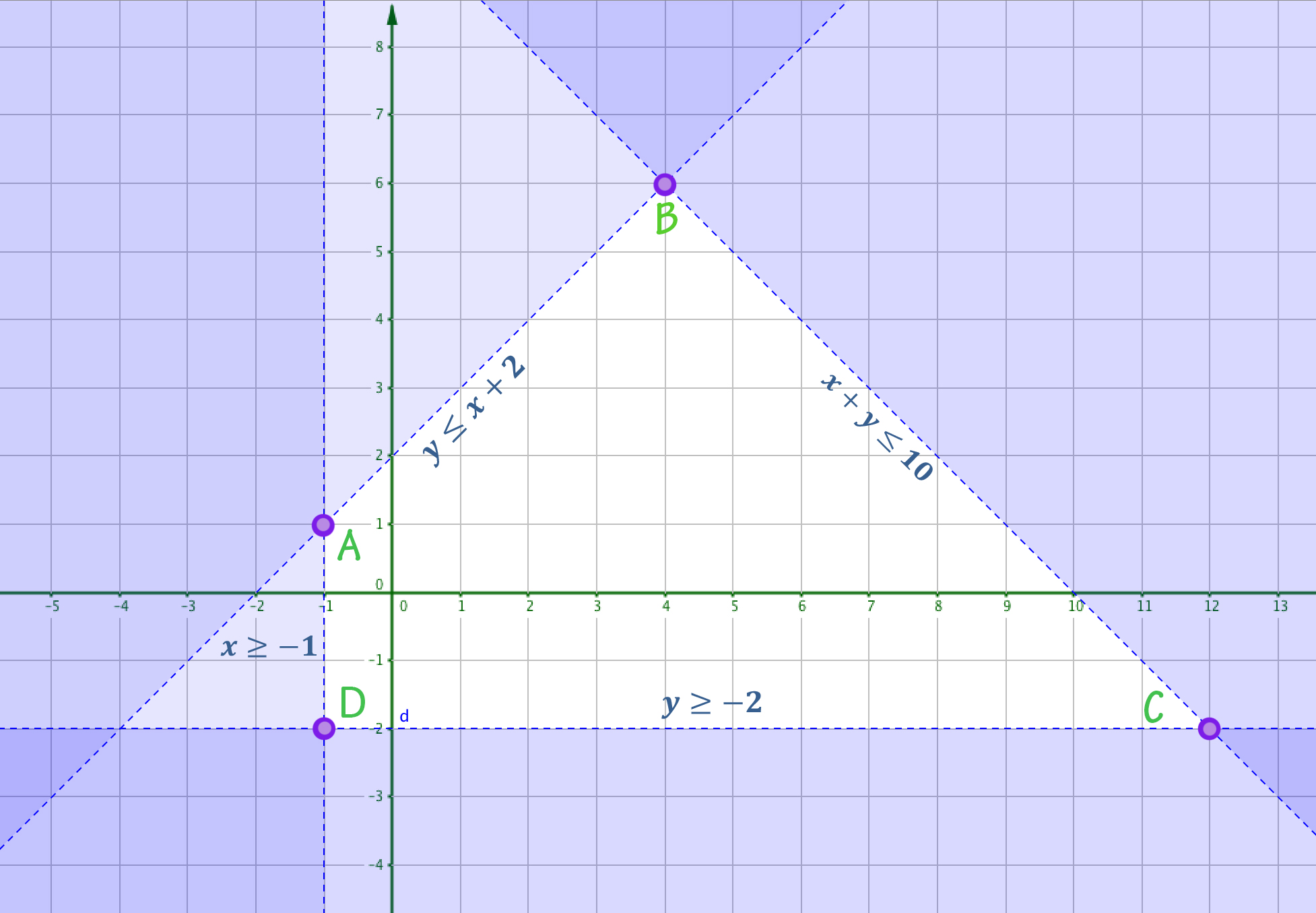
Los vértices se calculan:

 

       ⇒              ;         ⇒   

 

    ⇒           ;                ⇒  

 

 

(b)    Calculamos para cada vértice el valor que toma la función:

 

A ⇒

 

B ⇒  16   ⇒  Alcanza el máximo

 

C ⇒

 

D ⇒   ⇒  Alcanza el mínimo

 

La función alcanza el valor máximo en el punto B y el mínimo en el punto D.

 

Si añadimos la nueva restricción cambia la región factible:

 

 

 

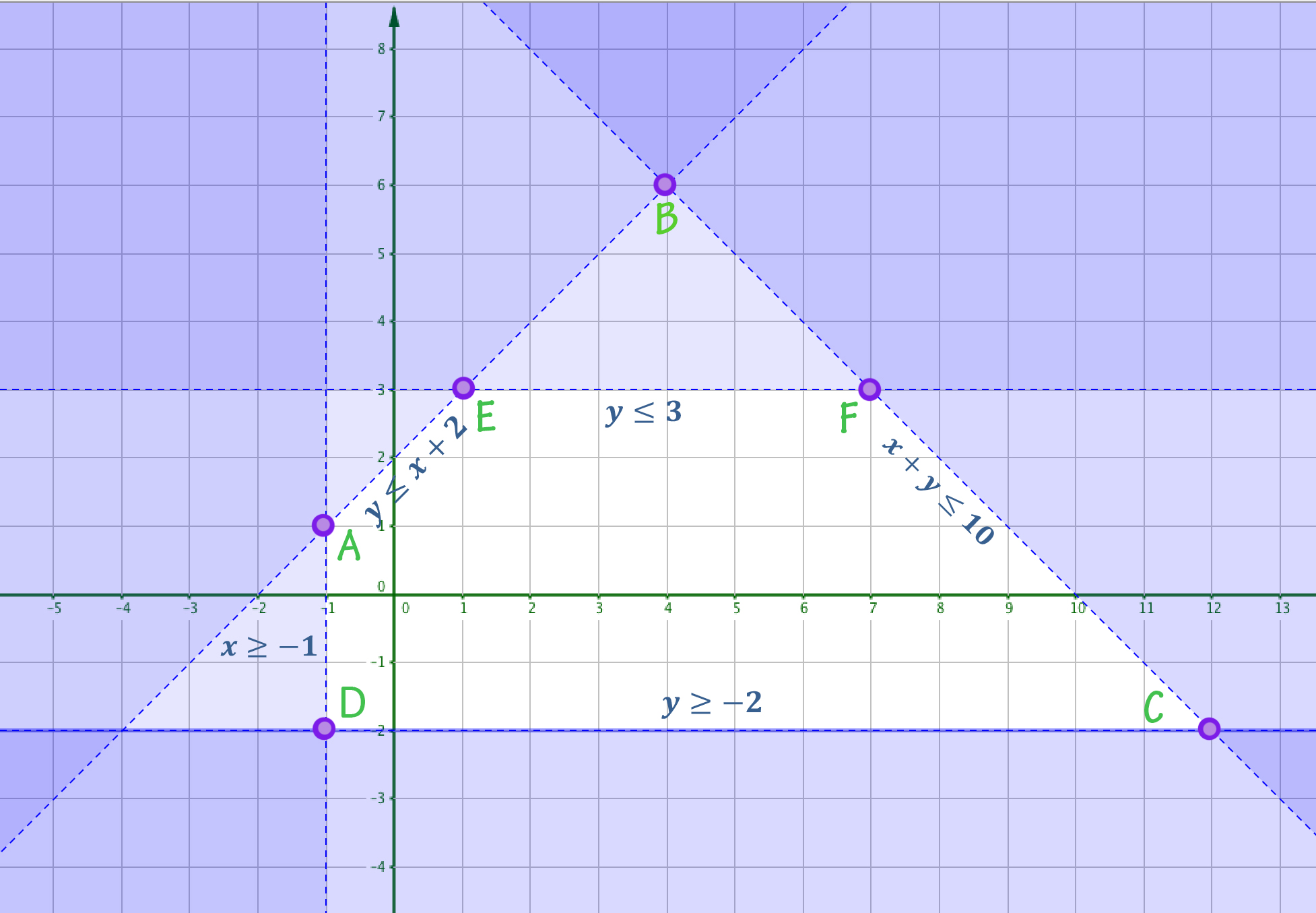
Desaparecería el vértice B y tendríamos otros dos nuevos vértices el E y el F:

       ⇒              ;         ⇒ 

 

 

Si calculamos el valor que toma la función en estos nuevos vértices nos queda:

 

E ⇒

 

F ⇒ 13   ⇒  Alcanza el máximo

 

Añadiendo la nueva restricción el máximo pasa de ser el punto (4,6) a ser el punto (7,3).