Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

4.    La    gráfica    de    una    función    f(x)    pasa    por   el   origen   de   coordenadas   y   su   derivada   es  . Determina la función f(x) y calcula los intervalos de concavidad y convexidad de f(x).

a)    Para calcularla función f(x) debemos obtener una primitiva de la función, es decir, tenemos que calcular su integral:

La hacemos por partes: 

La integral me quedaría:

La función f(x) será:

Nos queda calcular la constante de integración. Para eso, sabemos que la función pasa por el origen de coordenadas:

Por lo tanto, la función que buscamos sería:

Para calcular los intervalos de curvatura, necesito la segunda derivada. Como nos daban la primera, sólo tenemos que volver a derivar esta:

Para hacer los intervalos de curvatura necesitamos los posibles puntos de inflexión, que obtenemos igualando esta segunda derivada a cero:

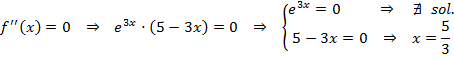
Con este valor y con el dominio que son todos los números reales, hacemos los intervalos de concavidad y convexidad y miramos el signo de la segunda derivada:

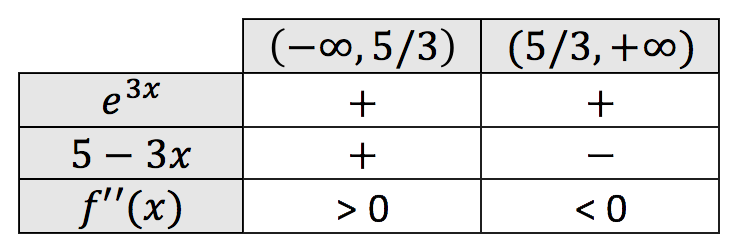
Por lo tanto los intervalos de curvatura son: