Galicia. Examen PAU resuelto de Matemáticas II. Septiembre 2015

3.     

a)   Define derivada de una función en un punto. Interpretación geométrica.

b) Dada la función  , calcula: intervalos de crecimiento y decrecimiento y máximos y mínimos relativos de f(x).

a)   La  derivada  de  una  función  real  en  un  punto  a  del  dominio  mide la variación en el incremento de la función alrededor del punto respecto de la variación en el incremento de la variable alrededor del punto. Si hacemos que esa variación tienda a cero tenemos la definición de derivada en un punto, que sería el siguiente límite: 

La interpretación geométrica de la derivada de una función en un punto coincide con la pendiente de la recta tangente en ese punto.

b)   El dominio  de  la  función  es  ,  ya  que  es producto de una función exponencial por una polinómica y a ambas podemos darles cualquier valor real. Para estudiar el crecimiento y decrecimiento hacemos la primera derivada e igualamos a cero:

El cero es por lo tanto un posible máximo o mínimo de la función. Con este punto vamos a estudiar el signo de la primera derivada:

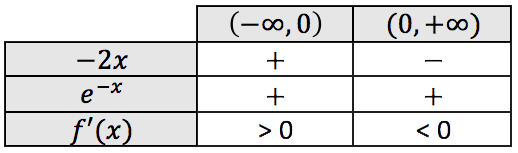
Los intervalos de crecimiento y decrecimiento son:

El posible máximo o mínimo relativo de la función es el x = 0, para comprobarlo, sustituimos este valor en la segunda derivada:

Por último, calculamos la otra coordenada del máximo relativo:

La función f(x) tiene un máximo relativo en el punto (0,2).