Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

3.     

a)   Definición e interpretación geométrica de la derivada de una función en un punto.

b)   Calcula los valores de b y c para que la función:

sea derivable en x = 0. (Nota: ln = logaritmo neperiano)

a)   La  derivada  de  una  función  real  en  un punto a del dominio mide la variación en el incremento de la función alrededor del punto respecto de la variación en el incremento de la variable alrededor del punto. Si hacemos que esa variación tienda a cero tenemos la definición de derivada en un punto, que sería el siguiente límite:

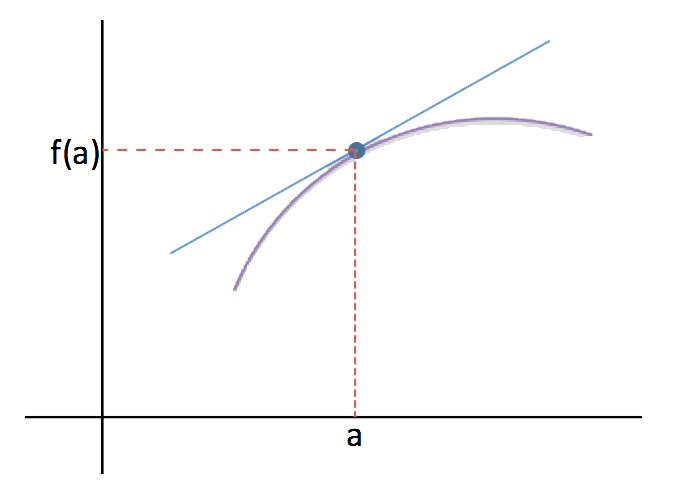
La interpretación geométrica de la derivada de una función en un punto coincide con la pendiente de la recta tangente en ese punto.

b)   Primero tenemos que estudiar la continuidad de la función en el punto x = 0, puesto que si la función no es continua en ese punto, no puede ser derivable:

Ahora estudiamos la derivabilidad en el punto x = 0. Para eso vamos a derivar la función:

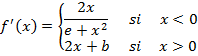
Ahora estudiamos la derivada por la izquierda y por la derecha en el punto:

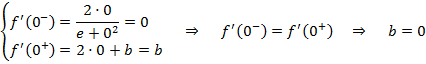
Por lo tanto para que la función sea derivable, b = 0 y c = 1.