Galicia. Examen PAU resuelto de Matemáticas II. Septiembre 2015

2.    Dadas las rectas 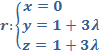   y  s:

 

a)   Estudia la posición relativa de r y s. Calcula la distancia de r a s.

b)  Si dos de los lados de un rectángulo están sobre las rectas r y s y dos vértices consecutivos del rectángulo son los puntos A(0,1,1) y B(0,4,4), calcula las coordenadas de los otros dos vértices y el área del rectángulo.

 

a)    En primer lugar, vamos a poner la recta s en las ecuaciones paramétricas, para ello, vamos a poner una de las incógnitas como parámetro, por ejemplo  , y resolvemos el sistema resultante:

Identificamos los puntos y los vectores de ambas rectas:

Con los puntos de las dos rectas hacemos un vector:  .

Ahora en una matriz vamos a poner los dos vectores directores y en otra los dos vectores directores y el vector que hicimos con los puntos de las rectas:

Calculamos los rangos y sabemos la posición relativa de las rectas:

La matriz A tiene rango 1, ya que los determinantes de orden 2 dan todos cero, al tener dos filas proporcionales. La matriz A^* tiene rango 2, porque hay determinantes de este orden distintos de cero:

Por lo tanto los vectores directores son linealmente dependientes, es decir, tienen la misma dirección. Por lo tanto, las rectas o bien son coincidentes o paralelas. Como el rango de la matriz ampliada es 2, quiere decir que el vector que hacemos con un punto de cada recta no tiene la misma dirección que los vectores directores, por lo que las rectas solo pueden ser paralelas.

Calcular la distancia entre dos rectas paralelas es lo mismo que calcular la distancia de un punto de una recta a la otra recta. La fórmula sería la siguiente:

Calculamos el módulo del vector director de la recta r:

El vector    ya lo tenemos calculado, hacemos el producto vectorial y el módulo del mismo:

Con todo lo calculado, podemos obtener la distancia entre las dos rectas:

 

b)   Los puntos A y B están sobre la recta r, porque estos puntos cumplen la ecuación de esta recta:

El dibujo del rectángulo y la colocación de los vértices sobre las rectas sería el siguiente:

Lo primero, vamos a coger un punto genérico de la recta s, este punto estaría formado por las coordenadas paramétricas de dicha recta:

La distancia de este punto al punto A o al punto B tiene que ser igual a la distancia entre las rectas. Por lo tanto:

Estas distancias coinciden con la distancia calculada en el apartado anterior entre las dos rectas:

Con los valores de  obtenidos, vamos a la recta s y obtenemos los vértices C y D que nos faltaban del rectángulo:

Para calcular el área ya conocemos la altura del rectángulo, puesto que sería la distancia entre el punto A y D o entre el punto B y C, que es la misma que la distancia entre las dos rectas. Para saber lo que mide la base, vamos a calcular la distancia entre los puntos A y B:

Mide lo mismo que la altura, por lo que es un cuadrado. Calculamos su área: