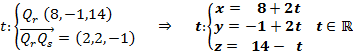Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

2.    Dadas las rectas 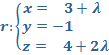   y  s:

 

a)   Estudia su posición relativa. Calcula la ecuación implícita o general del plano que pasa por el origen de coordenadas y es paralelo a r y a s.

b)   Calcula las ecuaciones paramétricas de la recta que corta perpendicularmente a r y a s.

 

a)    Identificamos los puntos y los vectores de ambas rectas:

 

Con los puntos de las dos rectas hacemos un vector:  .

Ahora en una matriz vamos a poner los dos vectores directores y en otra los dos vectores directores y el vector que hicimos con los puntos de las rectas:

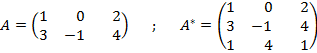
Calculamos los rangos y sabemos la posición relativa de las rectas:

La matriz A tiene rango 2, ya que:  .

 

Por lo tanto los vectores directores son linealmente independientes, es decir, no tienen la misma dirección. Por lo tanto las rectas sólo pueden ser o secantes o cruzadas.

La matriz A^* tiene rango 3, ya que:  .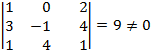

 

Por lo que el vector que hicimos con los puntos de ambas rectas no está en el mismo plano que el de los vectores directores. Por consiguiente las rectas son cruzadas.

Si el plano tiene que ser paralelo a las rectas r y s, los vectores directores de las mismas van a ser vectores que nos determinen el plano. Como además tiene que pasar por el origen de coordenadas, ya tenemos determinado nuestro plano:

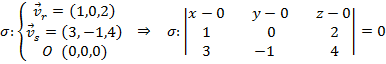
Resolviendo obtenemos el plano pedido:  .

b)   Lo que nos piden es la perpendicular común a dos rectas que se cruzan. Para eso vamos a poner las dos rectas en paramétricas. Una ya la teníamos y la otra como tenemos un punto y un vector director, la podemos poner directamente:

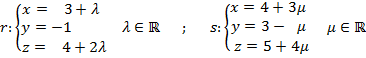
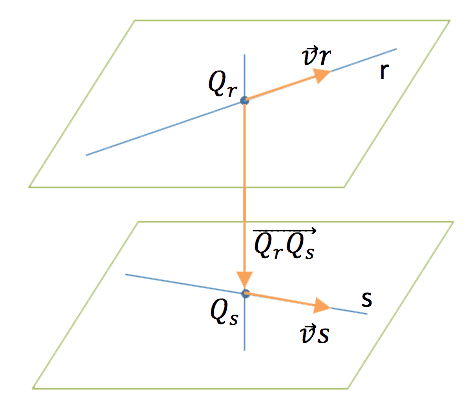
Ahora, vamos a coger un punto genérico de cada una de las dos rectas:

Hacemos un vector con estos dos puntos:

 

Este vector vamos a asegurarnos que sea perpendicular a los vectores directores de cada una de las rectas. Eso lo hacemos con el producto escalar:

Resolvemos el producto escalar y nos queda un sistema:

Estos valores son los que hacen que el vector  sea perpendicular a los vectores directores de las rectas. Vamos a calcularlo:

Sólo nos falta un punto para tener determinada la recta. Nos vale, tanto  como , pero nos llega con uno de los dos:

Con el punto y el vector tenemos determinada la recta perpendicular: