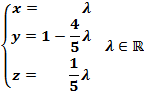Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

1.     

a)   Discute, según los valores del parámetro m, el sistema:

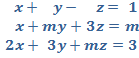
b)   Resuélvelo, si es posible, para  .

a)    Planteamos dos matrices, la de coeficientes (A) y la ampliada con los términos independientes (A^*):

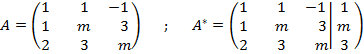
Calculamos el determinante de la matriz A y lo igualamos a cero para saber qué valores anulan dicho determinante y poder así discutir los rangos:

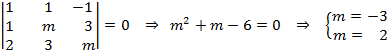
Los casos que tenemos son:

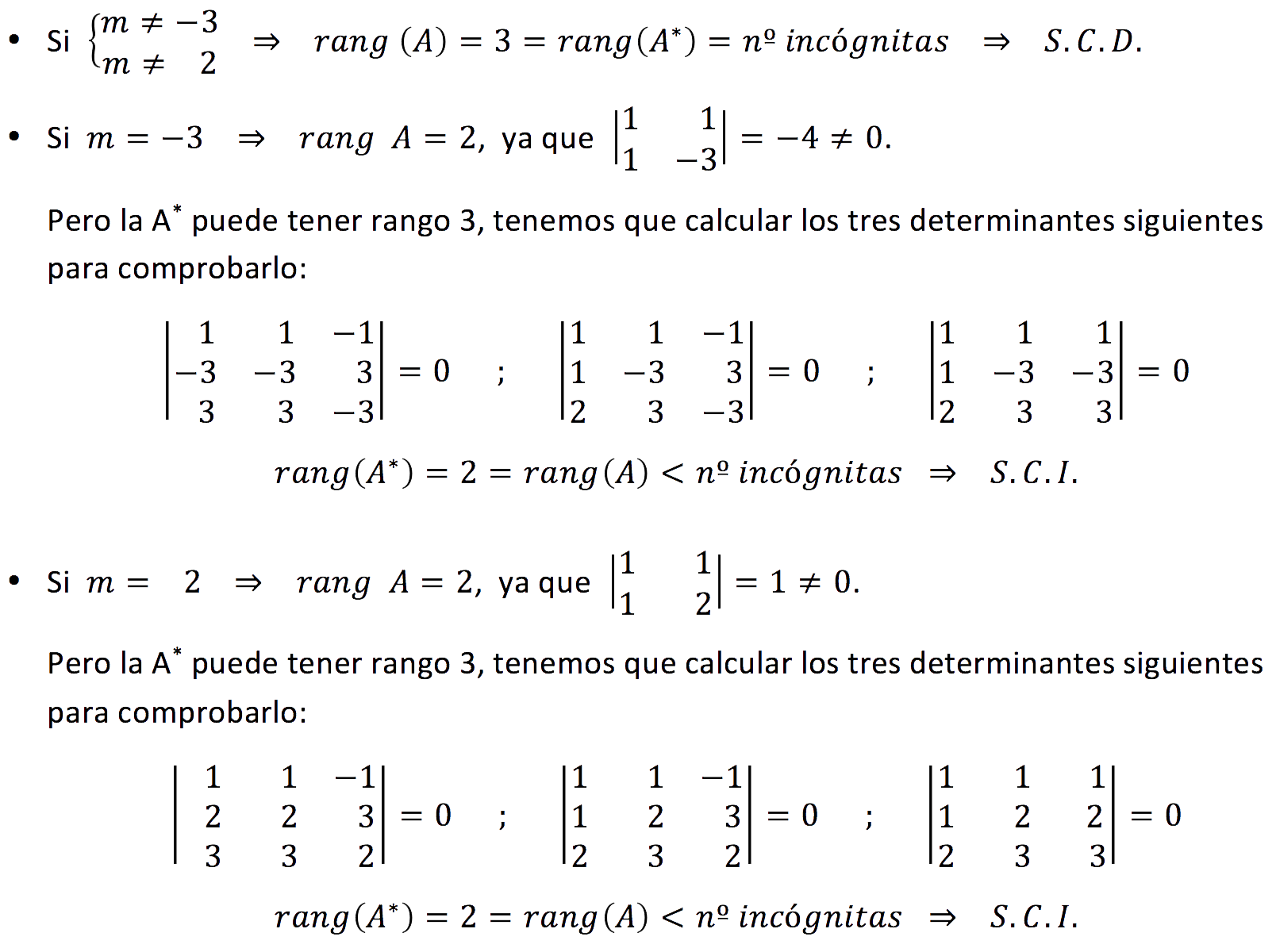
b)   Para el caso de    el sistema es compatible indeterminado, por lo tanto una de las ecuaciones es combinación lineal de las otras. Se ve, por ejemplo, que si sumamos la primera y la segunda obtenemos la tercera. La última es por tanto combinación lineal de las dos anteriores. Por eso podemos eliminar cualquiera de las dos primeras:

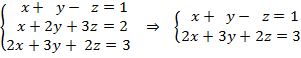
Ahora ponemos una de las incógnitas como parámetro y resolvemos por la regla de Cramer:

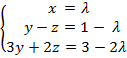
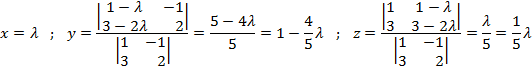
La solución del sistema para    es: