Galicia. Examen PAU resuelto de Matemáticas II. Septiembre 2015

4.  Dibuja y calcula el área de la región limitada por las gráficas de la parábola    y las rectas tangentes a la gráfica f(x) en los puntos correspondientes a x = 0 y x = 2 (Nota: para el dibujo de la gráfica de la parábola, indicar los puntos de corte con los ejes de coordenadas, su vértice y la concavidad o convexidad).

Vamos a calcular las rectas tangentes a la parábola. Primero calculamos las imágenes de los puntos:

Ahora las pendientes, con la derivada de la función en eses puntos:

La ecuación de la recta tangente a una función en un punto  , es:

Las ecuaciones de las dos rectas tangentes son:

Hacemos los cálculos para dibujar la parábola:

Corte eje OX:  y=0

Corte eje OY:  x=0

   ⇒   Punto de corte : 

Vértice:

Curvatura:

La parábola es cóncava ya que  .

Vamos a calcular el punto de corte entre las dos rectas:

Con todos estos datos podemos hacer el dibujo e identificar el área a calcular:

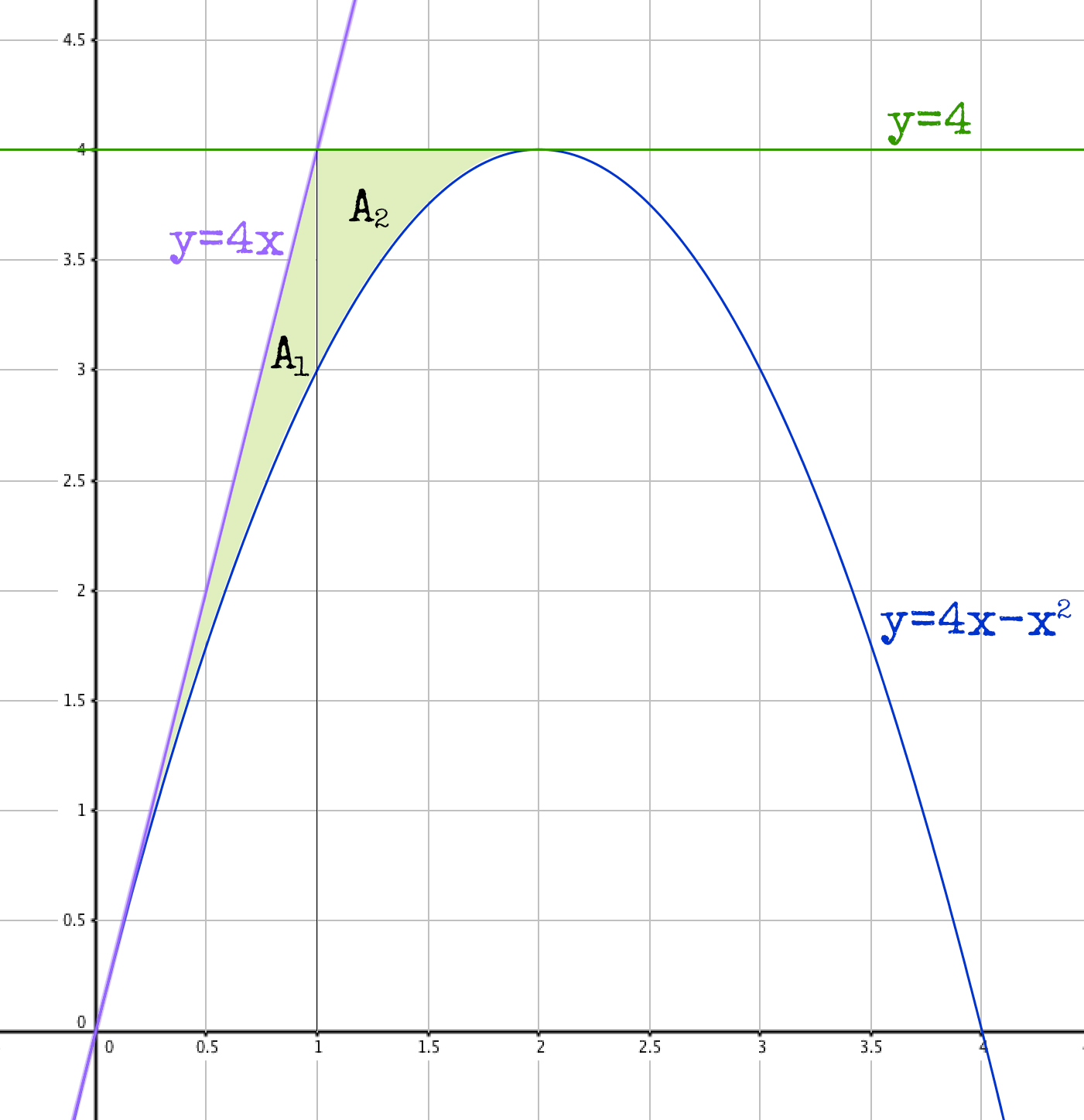
El área que limitan las rectas tangentes y la parábola es la coloreada de verde. La dividimos en dos partes porque por la parte de arriba esa área esta limitada rectas distintas. El área A₁ está limitada por la recta y = 4x y la parábola y el área A₂ por la recta y = 4 y la parábola.

Calculamos la primera área:

Ahora calculamos la segunda área:                                                                                                                                                                                                                       

Por lo tanto el área que nos piden es: