Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

4.     

a)   Define primitiva de una función y enuncia la regla de Barrow.

b)   Dada la función  , determina a, b y c sabiendo que    es la gráfica tangente a la gráfica f(x) en el punto correspondiente a la abscisa  x = 0  y que  .

a)    La definición de primitiva de una función sería:

Decimos que F(x) es una primitiva de una función f(x) si se cumple que  . Esto se denota:  . Si F(x) es primitiva de f(x), también lo es para todo . Por lo tanto podemos escribir:  .

El enunciado de la regla de Barrow es:

Si f(x) es una función continua en el intervalo [a,b], y F(x) una función definida en [a,b], derivable y primitiva de f(x), es decir, F’(x) = f(x), para cualquier , entonces:

b)   Si la recta tangente es y = 2x+1, la pendiente de la misma en el punto x = 0 es m = 2. Como la pendiente de la recta tangente a una función en un punto se calcula con la primera derivada, tenemos:

La función quedará entonces así:  .

Como la recta tangente y la función comparten el punto de tangencia, por medio de la recta podemos calcular la ordenada del punto x = 0:

El punto de tangencia es el punto (0,1). Como ese punto es de la función, se cumple:

Con estos valores la función queda:  .

Por último con el valor de la integral definida, calculamos el valor que falta:

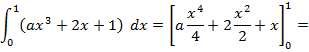
Por lo tanto los valores son: