Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

3.    Dibuja la gráfica de  =   estudiando: dominio, simetrías, puntos de corte con los ejes, asíntotas, intervalos de crecimiento y decrecimiento, máximos y mínimos relativos, puntos de inflexión e intervalos de concavidad y convexidad.

 

Vamos a ir calculando cada uno de los punto que nos piden:

Dominio: El dominio de una función racional son todos los valores reales, menos aquellos que anulan el denominador.

Simetrías:

La función par o función simétrica con respecto al eje OY  si cumple que :

No es función par o no tiene simetría con respecto al eje OY.

La función es impar o es simétrica con respecto al origen de coordenadas si cumple que  :

Tampoco es una función impar o simétrica con respecto al origen de coordenadas.

Puntos de corte con los ejes:

Cortes con el eje OX:  y = 0

Corta al eje OX en el punto (0,0).

Cortes con el eje OY:  x = 0

Corta al eje OY, también en el punto (0,0).

Asíntotas:

Asíntotas verticales: comprobamos la existencia en el punto que no es del dominio

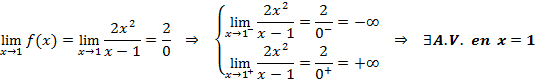
Asíntotas horizontales:

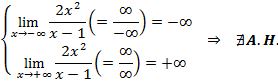
Asíntotas oblicuas:

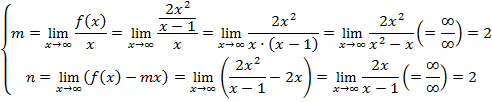
Crecimiento y decrecimiento: hacemos la primera derivada e igualamos a cero

Con estos puntos y con el domino miramos el signo de la primera derivada:

 

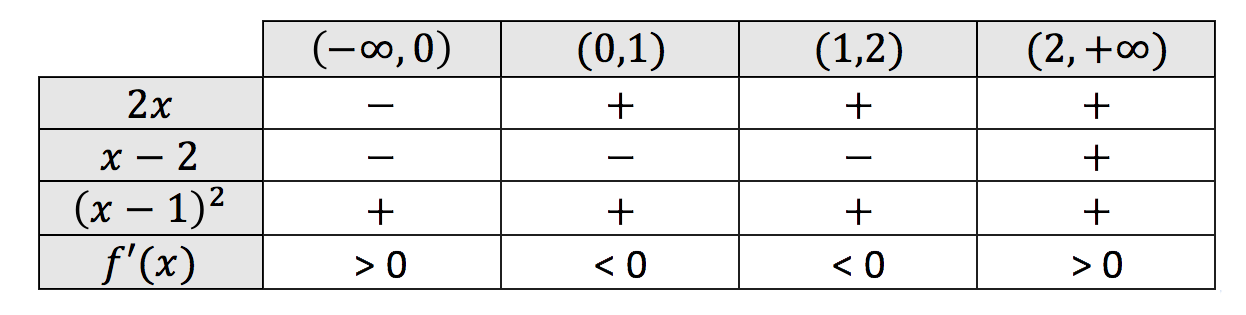
f(x) es creciente en: 

f(x) es decreciente en: 

Máximos y mínimos: los posibles máximos y mínimos relativos son el 0 y el 2, para saber si son extremos relativos, los substituimos en la segunda derivada.

Calculamos la segunda coordenadas de cada uno de los puntos:

Puntos de inflexión: igualamos la segunda derivada a cero para obtenerlos.

Al no tener solución la ecuación, no existen puntos de inflexión.

Concavidad y convexidad: para obtener los intervalos de la curvatura, al no haber puntos de inflexión, utilizamos simplemente el dominio de la función.

 

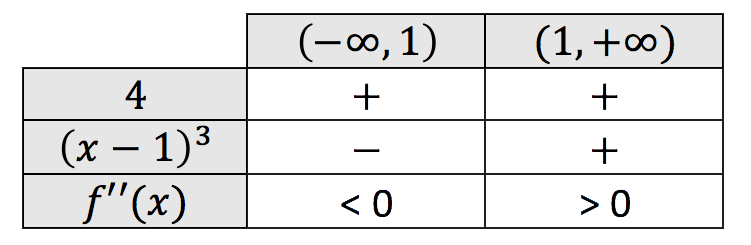
La función f(x) es cóncava en: 

La función f(x) es convexa en: 

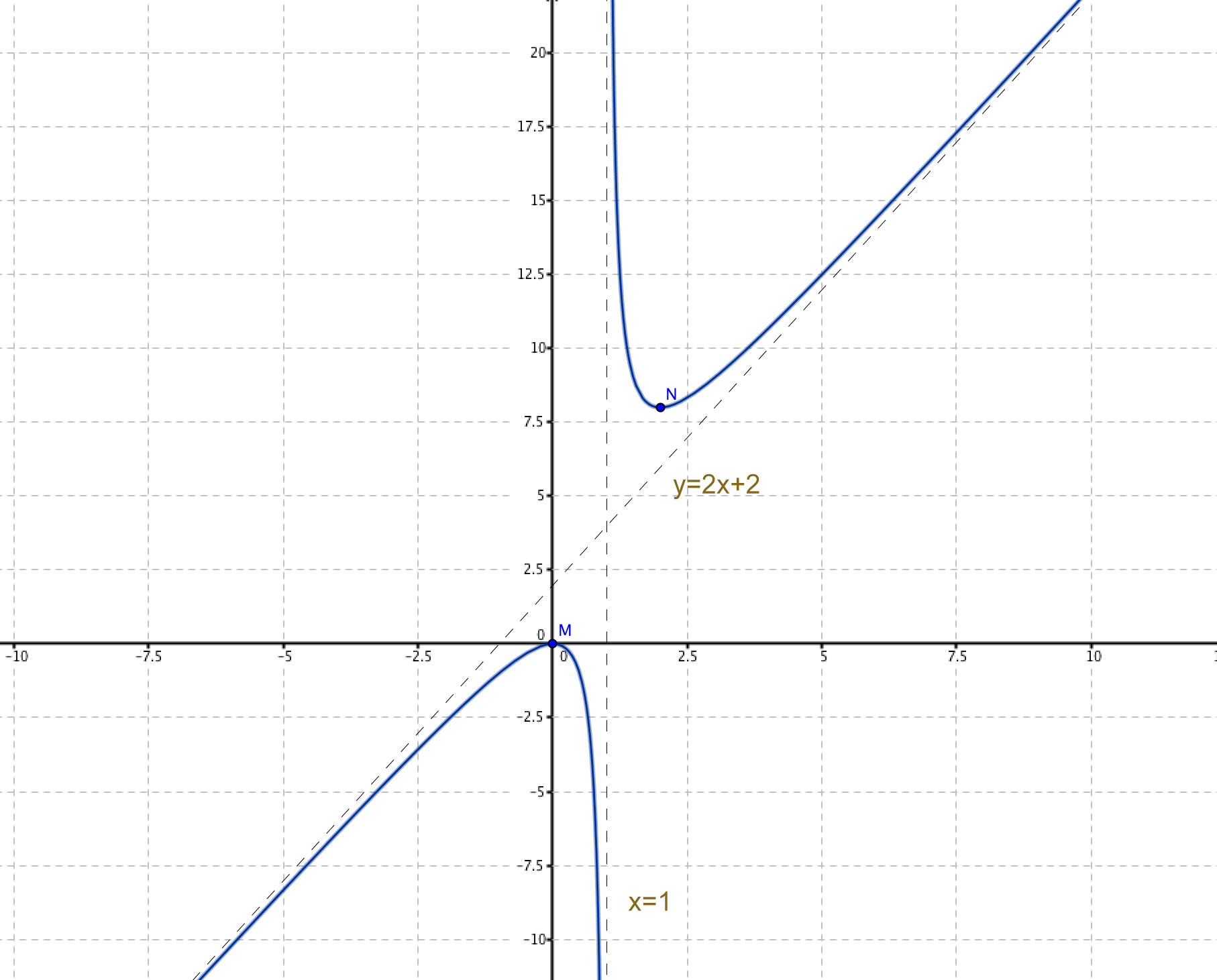
Representación gráfica: Con todo lo calculado anteriormente podemos trazar la gráfica de la función.