Galicia. Examen PAU resuelto de Matemáticas II. Junio 2015

2.    Dada la recta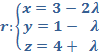 

a)   Determina la ecuación implícita del plano    que pasa por el punto    y es perpendicular a r. Calcula el punto de intersección de r y .

b)   Calcula la distancia del punto    a la recta r.

c)    Calcula el punto simétrico del punto    respecto a la recta r.

a)   Si el plano y la recta son perpendiculares, el vector director de la recta va a ser el vector normal del plano:

Sabiendo el vector normal podemos escribir:

Como ahora conocemos un punto del mismo, calculamos D y tenemos el plano que nos piden:

Para calcular el punto de intersección, primero substituimos las ecuaciones paramétricas de la recta en la ecuación general del plano para calcular el valor del parámetro:

Con este valor vamos a la recta y tenemos el punto:

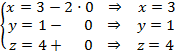
El punto de corte de r y  es: 

b)   Como el punto P es un punto del plano, el punto más próximo a él de la recta r, es el que acabamos de calcular en el apartado anterior. Por lo tanto, la distancia entre el punto P y la recta r es igual a  la distancia entre los puntos P y M:

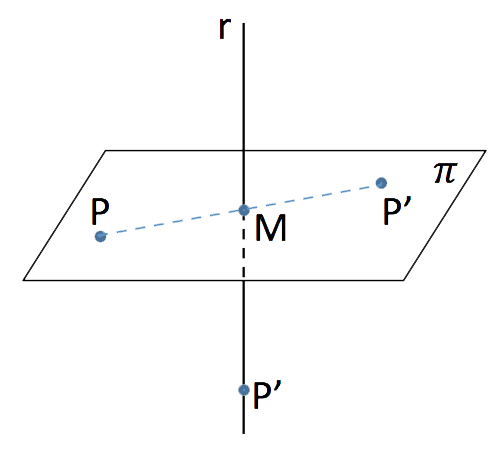
c)    El punto M, que era el punto de corte de la recta y el plano, va a ser el punto medio del punto P y de su simétrico P’. Por lo tanto, aprovechamos esta circunstancia para calcularlo: