Galicia. Examen PAU resuelto de Matemáticas II. Junio 2014

b)   ¿Coincide A con su inversa para algún valor de m?.

c)    Determina una matriz simétrica X de orden 2 tal que    y el determinante de la matriz 3X sea  .

a)    Vamos a calcular el rango de la matriz por determinantes. Empezamos calculando el determinante de orden 3 y vemos para qué valor de m se anula:

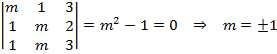
Discutimos en función de los valores de m:

· Si  , el determinante de orden 3 es distinto de cero, por lo tanto el rango es 3.

· Si  , el rango es 2, porque hay algún determinante de orden 2 distinto de cero.

· Si  , el rango es 2, porque hay algún determinante de ese orden distinto de cero:

b)   Si A coincide con su inversa, sabemos:

Calculamos entonces el cuadrado de la matriz A y vemos si puede ser igual a la matriz identidad, para algún valor de m:

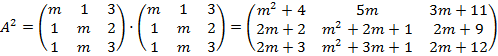
Por lo tanto, para que la matriz A coincidiera con su inversa, se debería cumplir:

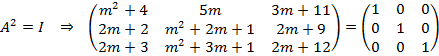
Vemos que esta igualdad no se puede cumplir, porque por ejemplo, el primer elemento de la primera matriz nunca puede ser igual al primero de la segunda:

No hay ningún valor de m que haga que la matriz coincida con su inversa.

c)    Una matriz simétrica es aquella que coincide con su traspuesta, por ejemplo:  .

Aplicando entonces la primera condición:

De la segunda condición sacamos otra ecuación:

Al final tenemos un sistemas de tres ecuaciones con tres incógnitas:

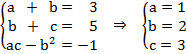
Por lo tanto, la matriz pedida es: