Galicia. Examen PAU resuelto de Matemáticas II. Junio 2014

3.  a)   Dada la función    calcula los valores de a, b, c sabiendo que    es una asíntota

            vertical y que    es la recta tangente a la gráfica en el punto correspondiente a x = 1.

            Para los valores de a, b, c calculados, ¿posee f(x) más asíntotas?

b)   Enuncia el teorema del valor medio del cálculo diferencial. ¿Se puede aplicar en el intervalo [0,1], este teorema a la función   ? En caso afirmativo, calcula el punto al que hace referencia el teorema.

a)    Si x = 1/2 es una asíntota vertical de la función, es porque ese punto no es del dominio de la misma. Como en las funciones racionales los puntos que no son del dominio son los que anulan el denominador:

Si la recta tangente en el punto x = 1 es  , la pendiente de la misma es 5. Por lo tanto sabemos que:  . Entonces hacemos la derivada de la función:

Como además el punto x = 1 es tanto de la función como de la recta tangente, de la recta podemos calcular la segunda coordenada del punto:

El punto de tangencia es el  . Este punto también es un punto de la función:

Con estas dos ecuaciones, resolvemos el sistema y obtenemos los valores de a y b:

La función, con los valores de a, b y c calculados quedaría así:

Vamos a estudiar si tiene asíntotas horizontales:

Si tiene asíntotas horizontales, no tiene asíntotas oblicuas.

b)   Si f(x) es una función continua en [a,b] y derivable en (a,b), entonces existe al menos un    tal que  .

La función dada es continua en  , por lo tanto es continua en el intervalo [0,1]. Lo mismo ocurre con la derivabilidad, es derivable en el intervalo (0,1). Entonces sí se puede aplicar el teorema y va a existir al menos un    tal que:

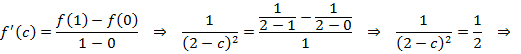
De los dos valores obtenidos, sólo nos vale el segundo, ya que el otro no se encuentra en el intervalo de aplicación del teorema. Por lo tanto, el valor al que hace referencia el teorema es  .