Galicia. Examen PAU resuelto de Matemáticas II. Junio 2014

 2.   a)   Define  el  producto  vectorial  de  dos vectores. Dados los vectores  ,  ,

             calcula los vectores unitarios y perpendiculares a los dos vectores    y  .

b) Calcula  el  valor  de  a  para  que  la  recta      no  corte   al   plano  .  Para ese valor de a, calcula la distancia de la recta al plano.

a)    El  producto  vectorial  de  dos  vectores,     y  , es otro vector cuya dirección es perpendicular a los dos vectores y su sentido sería igual al avance de un sacacorchos al girar de   a  :

Para calcular un vector perpendicular a dos vectores dados, necesitaremos hacer el producto vectorial de los mismos:

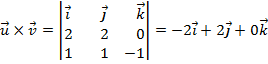
Así tenemos un vector perpendicular, para tener el otro, simplemente tendríamos que hacer el producto vectorial de  , que nos daría el mismo vector, pero con sentido contrario. Por lo tanto los dos vectores perpendiculares son:    y  . Ahora necesitamos que sean unitarios, es decir, que tengan de módulo la unidad. Para eso calculamos su módulo y dividimos cada una de sus coordenadas entre él:

b)   Lo primero que vamos a hacer es poner la recta en las ecuaciones paramétricas:

Ahora, para calcular la posición relativa de la recta y del plano, substituimos las ecuaciones paramétricas de r en el plano:

Si    no obtenemos valor para  y la recta y el plano serán paralelos. De aquí sacamos que el valor para el que eso se cumple es a = 1.

Con ese valor el plano nos queda:   y podemos calcular la distancia del mismo a la recta. Simplemente esa distancia coincide con la distancia entre un punto de la recta y el plano: