Galicia. Examen PAU resuelto de Matemáticas II. Junio 2014

OPCIÓN A

3.   a)   Define  función  continua  en  un  punto.  ¿Qué  tipo  de  discontinuidad  tiene     en  los

            puntos x = 0 y x = 2?

b)  Calcula la ecuación de la recta tangente a la gráfica de    en su punto de inflexión.

 

a)  Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:

                    I.     Que el punto x = a tenga imagen,  .

                  II.     Que exista el límite de la función en el punto x = a.

                III.     Que la imagen del punto coincida con el límite de la función en el punto:

Vamos a estudiar la continuidad de la función dada en los puntos indicados:

En x = 0:

                    I.     Imagen de la función en el punto:

                  II.     Límites laterales:

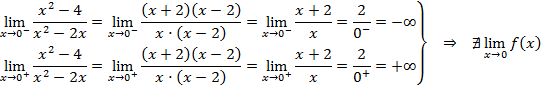
                III.   No existe la imagen del punto ni el límite, por lo tanto la función no es continua en x = 0 y presenta una discontinuidad inevitable de salto infinito, como indican los límites laterales.

En x = 2:

                    I.     Imagen de la función en el punto:

                  II.     Límites laterales:

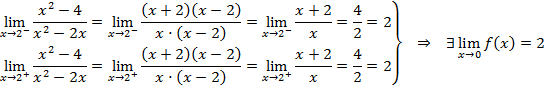
                III.   No existe la imagen del punto pero sí el límite, por lo tanto, la función no es continua y presenta una discontinuidad evitable en x = 2.

 

b) Primero necesitamos calcular el punto de inflexión, para ello igualamos a segunda derivada a cero y comprobamos en la tercera derivada que efectivamente ese punto o puntos son puntos de inflexión:

Por lo tanto en el punto x = 1 la función tiene un punto de inflexión. Calculamos la segunda coordenada del mismo:

El punto de inflexión está en el punto  . Necesitamos ahora la pendiente de la recta tangente en ese punto. La calculamos substituyendo la coordenada x del punto en la primera derivada:

Por lo tanto una vez tenemos la pendiente,  , y el punto, , ya podemos escribir la ecuación de la recta tangente: