Galicia. Examen PAU resuelto de Matemáticas II. Septiembre 2014
|
OPCIÓN A |
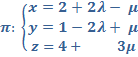 y la recta
y la recta
a) Estudia la posición relativa de ![]() y r. Si se cortan, calcula el punto de corte.
y r. Si se cortan, calcula el punto de corte.
b) Calcula el ángulo que forman ![]() y r. Calcula el plano que contiene a r y es perpendicular a
y r. Calcula el plano que contiene a r y es perpendicular a ![]() .
.
a) Vamos a calcular la ecuación general del plano:
.png)
Simplificado, el plano nos queda: ![]()
Ahora vamos a calcular las ecuaciones paramétricas de la recta r, para ello vamos a poner z como parámetro ![]() :
:
.png)
Para calcular la posición relativa de la recta y del plano, basta con substituir las ecuaciones de la recta en el plano:
![]()
Como obtenemos solución, la recta y el plano se cortan en un punto. Para calcularlo tenemos que substituir el valor obtenido de ![]() en las ecuaciones paramétricas de la recta:
en las ecuaciones paramétricas de la recta:
.png)
El punto de corte es el (0,3,4).
b) El ángulo que forman la recta y el plano lo calculamos a partir del vector director de la recta, ![]() , y el vector normal del plano, que lo sacamos de la ecuación general del mismo,
, y el vector normal del plano, que lo sacamos de la ecuación general del mismo, ![]() :
:
![]()
.png)
La recta y el plano se cortan formando un ángulo de 300.
Para calcular el plano que contiene a r y es perpendicular al plano ![]() , que le vamos a llamar
, que le vamos a llamar ![]() , tenemos dos vectores, uno el vector director de r y otro el vector normal de
, tenemos dos vectores, uno el vector director de r y otro el vector normal de ![]() . Además cualquier punto de la recta r va a pertenecer al plano
. Además cualquier punto de la recta r va a pertenecer al plano ![]() , con lo que ya tenemos determinado el plano:
, con lo que ya tenemos determinado el plano:
.png)

